`y=2sin x +2cos x-2sin 2x`
`<=>y=2(sin x+cos x-2sin x cos x)`
Đặt `sin x +cos x=t` `t in [-\sqrt{2};\sqrt{2}]`
`=>2sin x cos x=t^2-1`
H/s có dạng: `y=2(t-t^2+1)=-2t^2+2t+2`
Xét `y=-2t^2+2t+2` có: `I(1/2;5/2)`
BBT:
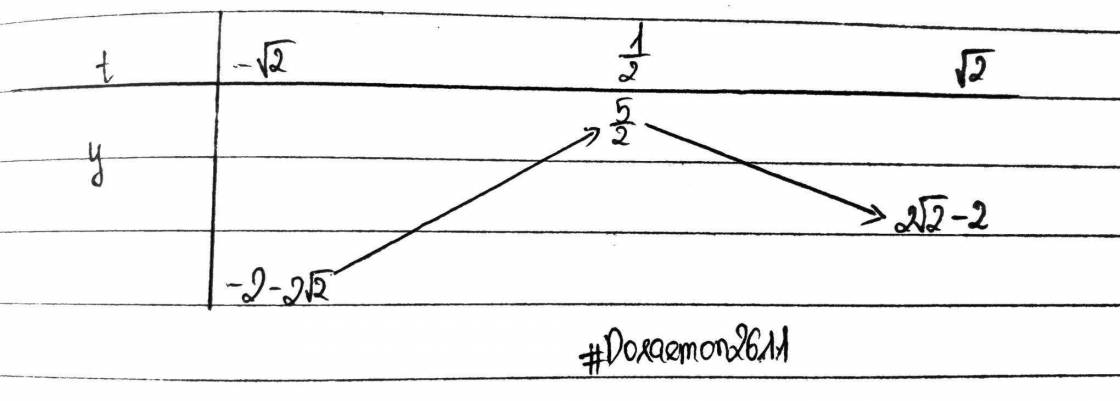
`=>y_[mi n]=-2-2\sqrt{2}<=>t=-\sqrt{2}<=>sin x +cos x=-\sqrt{2}`
`<=>sin(x+\pi/4)=-1<=>x+\pi/4=-\pi/2+k2\pi<=>x=-[3\pi]/4+k2\pi` `(k in ZZ)`
`y_[max]=5/2<=>t=1/2<=>sin (x+\pi/2)=\sqrt{2}/4` `(sin \alpha=\sqrt{2}/4)`
`<=>[(x+\pi/2=\alpha+k2\pi),(x+\pi/2=\pi-\alpha+k2\pi):}`
`<=>[(x=\alpha-\pi/2+k2\pi),(x=\pi/2-\alpha+k2\pi):}` `(k in ZZ)`

