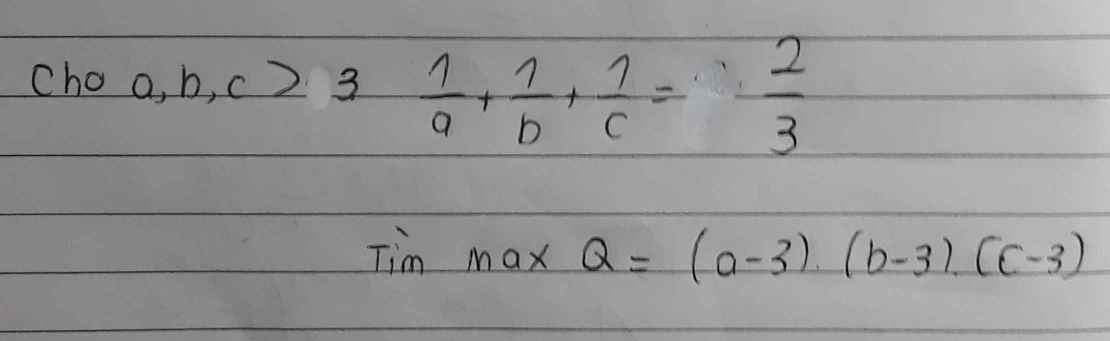Đặt \(\left(a-3;b-3;c-3\right)=\left(x;y;z\right)>0\)
\(\dfrac{1}{x+3}+\dfrac{1}{y+3}+\dfrac{1}{z+3}=\dfrac{2}{3}\)
\(\Leftrightarrow\dfrac{3}{x+3}+\dfrac{3}{y+3}+\dfrac{3}{z+3}=2\)
\(\Leftrightarrow\dfrac{3}{x+3}=1-\dfrac{3}{y+3}+1-\dfrac{3}{z+3}=\dfrac{y}{y+3}+\dfrac{z}{z+3}\ge2\sqrt{\dfrac{yz}{\left(y+3\right)\left(z+3\right)}}\)
Tương tự: \(\dfrac{3}{y+3}\ge2\sqrt{\dfrac{xz}{\left(x+3\right)\left(z+3\right)}}\) ; \(\dfrac{3}{z+3}\ge2\sqrt{\dfrac{xy}{\left(x+3\right)\left(y+3\right)}}\)
Nhân vế:
\(\dfrac{27}{\left(x+3\right)\left(y+3\right)\left(z+3\right)}\ge\dfrac{8xyz}{\left(x+3\right)\left(y+3\right)\left(z+3\right)}\)
\(\Rightarrow Q=xyz\le\dfrac{27}{8}\)
Đúng 1
Bình luận (0)
