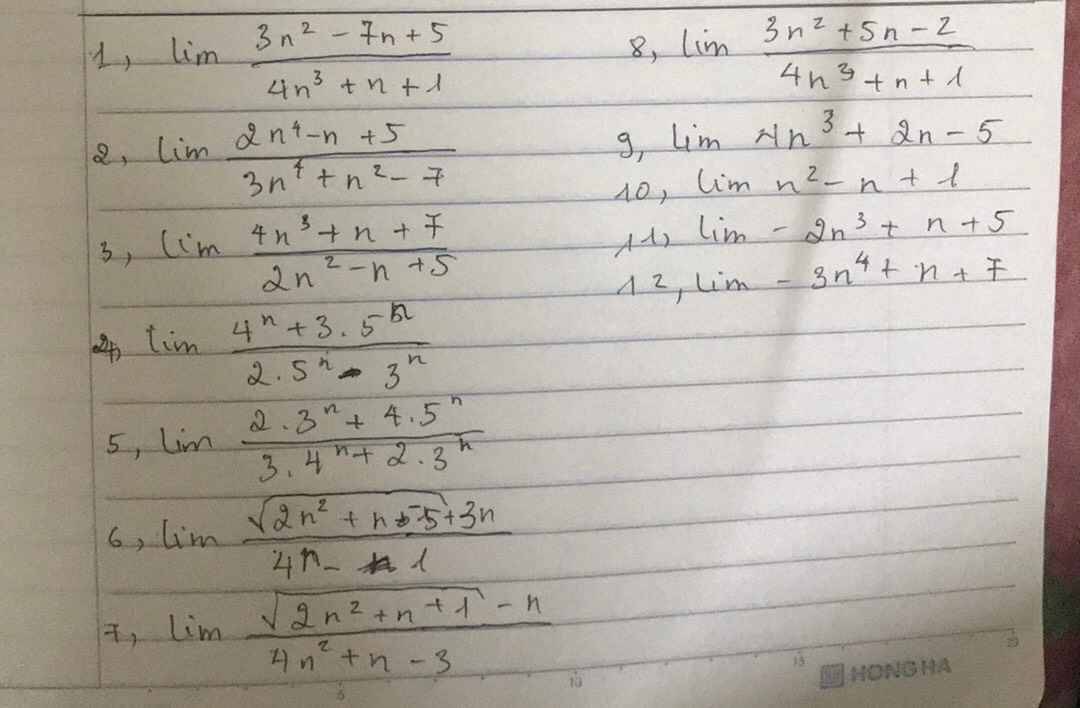Tết này nghỉ sớm đi học hành gì nữa trời :v
Câu 24 là dãy truy hồi, có phương pháp biến đổi, 1 là bạn lên mạng search phương pháp hoặc để tối tui rảnh tui làm cho
Câu 25 thì tính tổng dãy dưới mẫu là xong, dãy đó là một csn với số hạng đầu là 1 và công bội =n^2. Tính tổng rồi rút gọn tính lim là được
Thoi giup luon :v
\(v_n=u_n-1\Rightarrow\left\{{}\begin{matrix}v_1=u_1-1=2-1=1\\v_{n+1}=\dfrac{1}{2}v_n\end{matrix}\right.\)
\(\Rightarrow v_n=1.\left(\dfrac{1}{2}\right)^{n-1}\Rightarrow u_n=v_n+1=\dfrac{1}{2^{n-1}}+1\)
\(\Rightarrow\lim\limits u_n=\lim\limits\left(\dfrac{2}{2^n}+1\right)=\lim\limits\dfrac{2+2^n}{2^n}=1\)
2/ Tui vua moi nghi lai va nhan ra cach nay hay hon cach ban sang tui nghi nen tui lam cach nay nha :v
\(u_n=\dfrac{n}{\left(n^2\right)^2+2n^2+1-n^2}=\dfrac{n}{\left(n^2+1\right)^2-n^2}=\dfrac{n}{\left(n^2+1-n\right)\left(n^2+1+n\right)}\)
\(u_1=\dfrac{1}{\left(1+1-1\right)\left(1+1+1\right)}=\dfrac{1}{1.3}\Rightarrow2u_1=\dfrac{2}{1.3}=\dfrac{1}{1}-\dfrac{1}{3}\)
\(2u_2=\dfrac{2.2}{\left(4+1-2\right)\left(4+1+2\right)}=\dfrac{2.2}{3.7}=\dfrac{1}{3}-\dfrac{1}{7}\)
\(2u_3=\dfrac{3.2}{\left(9+1-3\right)\left(9+1+3\right)}=\dfrac{3.2}{7.13}=\dfrac{1}{7}-\dfrac{1}{13}\)
........
\(\Rightarrow2u_n=\dfrac{1}{n^2+1-n}-\dfrac{1}{n^2+1+n}\)
\(\Rightarrow2(u_1+u_2+u_3+....+u_n)=\dfrac{2}{1.3}+\dfrac{2.2}{3.7}+\dfrac{3.2}{7.13}+...+\dfrac{2n}{\left(n^2+1-n\right)\left(n^2+1+n\right)}\)
\(=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{13}+...+\dfrac{1}{n^2+1-n}-\dfrac{1}{n^2+1+n}\)
\(=1-\dfrac{1}{n^2+1+n}\)
\(\Rightarrow\lim\limits_{n\rightarrow+\infty}\left(u_1+u_2+...+u_n\right)=\lim\limits\dfrac{1}{2}.\left(1-\dfrac{1}{n^2+1+n}\right)=\lim\limits\dfrac{1}{2}.\left(\dfrac{n^2+n}{n^2+1+n}\right)=\lim\limits\dfrac{1}{2}.1=\dfrac{1}{2}\)