\(\sqrt{x^2-4}-x+2=0\) (ĐK: \(\left\{{}\begin{matrix}x\ge2\\x\le-2\end{matrix}\right.\))
\(\Leftrightarrow\sqrt{x^2-4}=x-2\)
\(\Leftrightarrow x^2-4=\left(x-2\right)^2\)
\(\Leftrightarrow x^2-4=x^2-4x+4\)
\(\Leftrightarrow x^2-x^2+4x=4+4\)
\(\Leftrightarrow4x=8\)
\(\Leftrightarrow x=\dfrac{8}{4}\)
\(\Leftrightarrow x=2\left(tm\right)\)
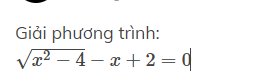




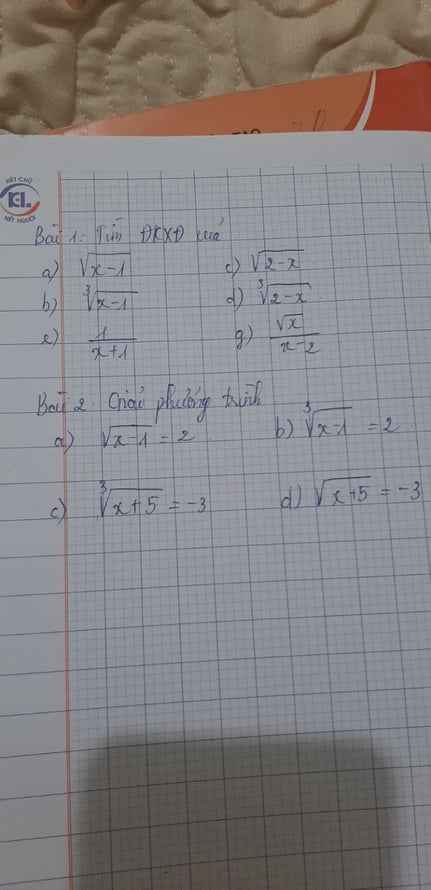 Giúp mình với ạ
Giúp mình với ạ