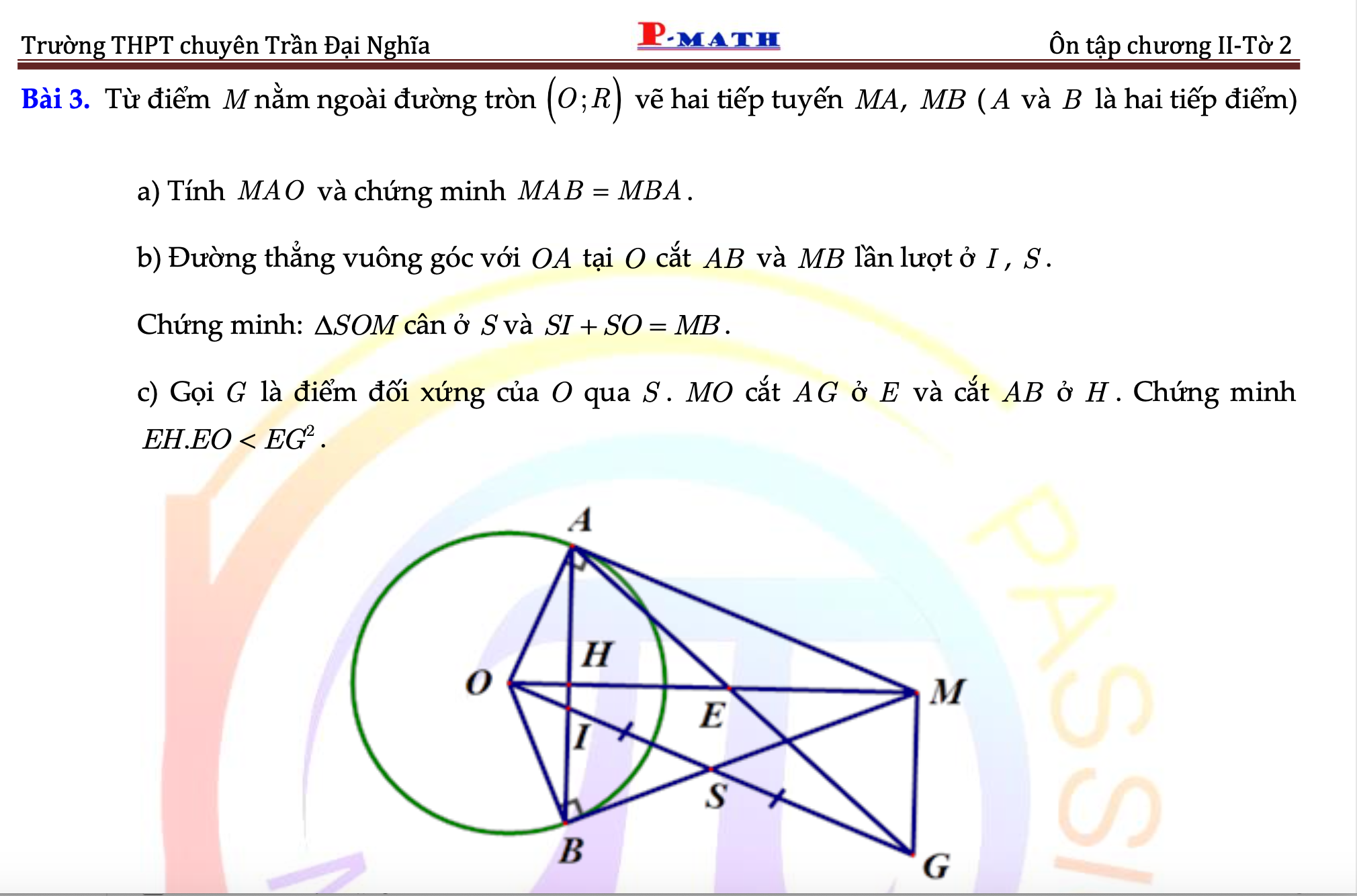
3: Đặt \(P=A:B\)
\(=\dfrac{x+2\sqrt{x}}{x-1}:\dfrac{\sqrt{x}+2}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}+2}\)
\(=\dfrac{x}{\sqrt{x}-1}\)
Để P>1 thì P-1>0
=>\(\dfrac{x-\sqrt{x}+1}{\sqrt{x}-1}>0\)
=>\(\sqrt{x}-1>0\)
=>\(\sqrt{x}>1\)
=>x>1
3) \(\dfrac{A}{B}>1\)
\(\Leftrightarrow\dfrac{x+2\sqrt{x}}{x-1}:\dfrac{\sqrt{x}+2}{\sqrt{x}\left(\sqrt{x}-1\right)}>1\)
\(\Leftrightarrow\dfrac{x+2\sqrt{x}}{x-1}.\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}+2}>1\)
\(\Leftrightarrow\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}+2}>1\)
\(\Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}+1}.\dfrac{\sqrt{x}}{1}>1\)
\(\Leftrightarrow\dfrac{x}{\sqrt{x}+1}-1>0\)
\(\Leftrightarrow\dfrac{x}{\sqrt{x}+1}-\dfrac{\sqrt{x}-1}{\sqrt{x}-1}>0\)
\(\Leftrightarrow x-\sqrt{x}+1>0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)^2>0\)
\(\Leftrightarrow\sqrt{x}-1>0\)
\(\Leftrightarrow x>1\)
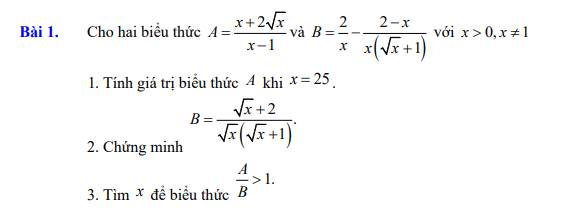



 ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn
ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn 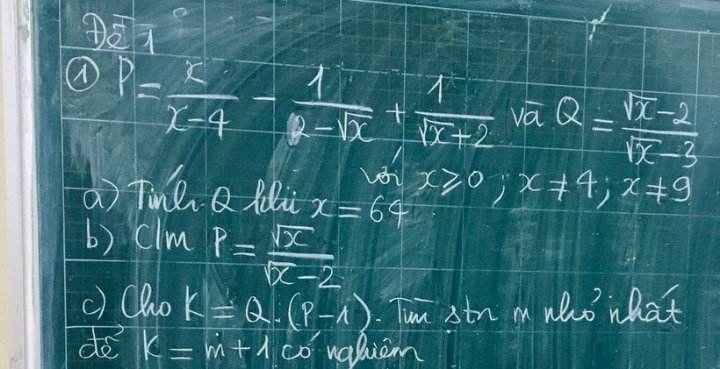 giúp mình câu c với ạ, mình cảm ơn nhiều
giúp mình câu c với ạ, mình cảm ơn nhiều