a: Theo đề, ta có hệ:
\(a\cdot\dfrac{1}{4-2\sqrt{3}}=\dfrac{1}{4-2\sqrt{3}}\)
=>a=1
=>y=x^2
e: PTHĐGĐ là:
x^2+2(m+3)x+2m-2=0
Δ=(2m+6)^2-4(2m-2)
=4m^2+24m+36-8m+8
=4m^2+16m+44
=4m^2+16m+16+28=(2m+4)^2+28>0
=>Phương trình luôn có 2 n0 pb
x1+x2=-2m-6; x1x2=2m-2
\(H=\dfrac{x_2^2+2x_2+1+x_1^2+2x_1+1}{\left(x_1+1\right)^2\left(x_2+1\right)^2}\)
\(=\dfrac{\left(-2m-6\right)^2-2\left(2m-2\right)+2\left(-2m-6\right)+2}{\left[2m-2-2m-6+1\right]^2}\)
\(=\dfrac{4m^2+24m+36-4m+4-4m-12+2}{49}\)
\(=\dfrac{4m^2+16m+30}{49}=\dfrac{4m^2+16m+16+14}{49}=\dfrac{\left(2m+4\right)^2+14}{49}>=\dfrac{2}{7}\)
Dấu = xảy ra khi m=-2
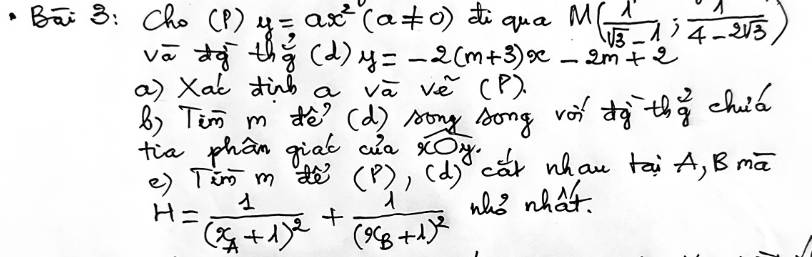



 làm giúp mik bài 4 câu a,b ạ,mik cảm ơn ạ
làm giúp mik bài 4 câu a,b ạ,mik cảm ơn ạ




