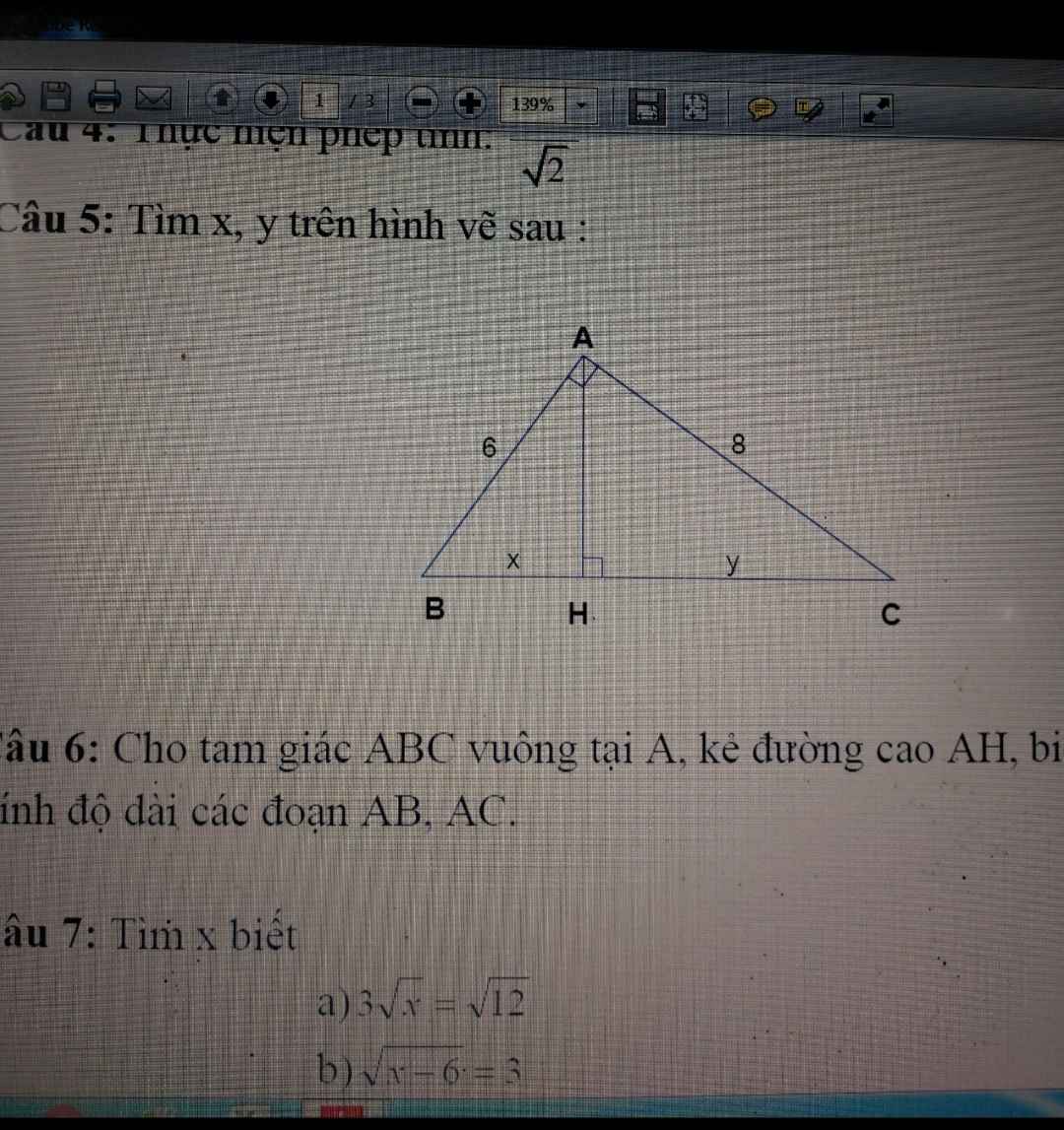
c: Xét tứ giác AEHF có
\(\widehat{EAF}=\widehat{AFH}=\widehat{AEH}=90^0\)
Do đó: AEHF là hình chữ nhật
Suy ra: AE=HF; AF=HE; AH=EF
Xét ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB
nên \(EA\cdot EB=HE^2\)
hay \(HE^2=EB\cdot HF\)
Xét ΔAHC vuông tại H có HF là đường cao ứng với cạnh huyền AC
nên \(FA\cdot FC=HF^2\)
hay \(HF^2=FC\cdot HE\)
Xét ΔFHE vuông tại H có
\(FE^2=FH^2+EH^2\)
hay \(AH^2=EB\cdot HF+FC\cdot HE\)
Đúng 1
Bình luận (1)
