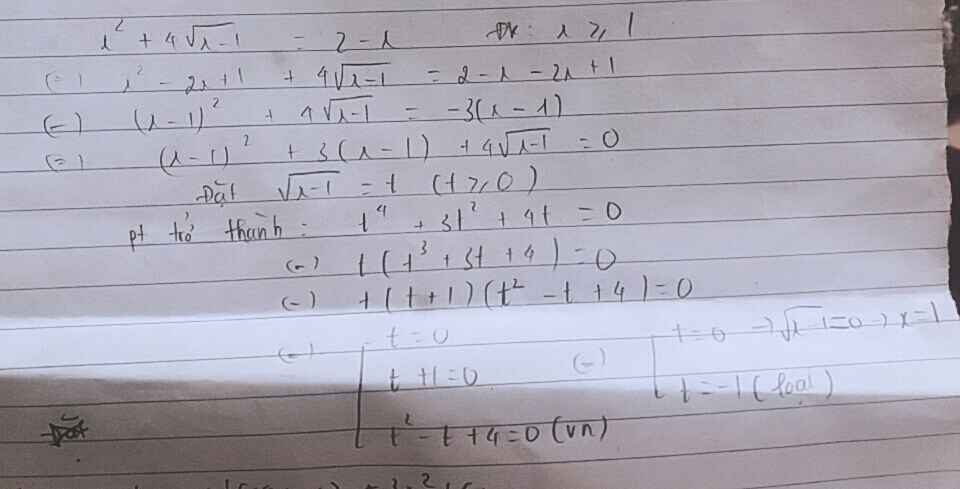Question

Giải pt:

\(x^2+4\sqrt{x-1}=2-x\)

Giúp mình nhanh nkaaa.

Answer 1

ĐKXĐ: \(x\ge1\)

\(x^2+x-2+4\sqrt{x-1}=0\)

\(\Leftrightarrow\left(x-1\right)\left(x+2\right)+4\sqrt{x-1}=0\)

Do \(x\ge1\Rightarrow\left\{{}\begin{matrix}\left(x-1\right)\left(x+2\right)\ge0\\\sqrt{x-1}\ge0\end{matrix}\right.\)

\(\Rightarrow\left(x-1\right)\left(x+2\right)+4\sqrt{x-1}\ge0\)

Đẳng thức xảy ra khi và chỉ khi:

\(\left\{{}\begin{matrix}\left(x-1\right)\left(x+2\right)=0\\\sqrt{x-1}=0\end{matrix}\right.\) \(\Rightarrow x=1\)

Answer 2

Kl:x=1

Answer 3

Cakpan làm thêm giúp mình theo này đc không ạ?

\(\Leftrightarrow x^2=2-x-2\sqrt{x-1}.2\)

\(\Leftrightarrow x^2+x-1+4=2-x+x+1-2\sqrt{x-1}.2+4\)

\(\Leftrightarrow x^2+x+x-1-2+4=\left(\sqrt{x-1}+2\right)^2\)

.......