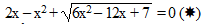Đặt \(\sqrt{6x^2-12x+7}=t>0\Rightarrow x^2-2x=\dfrac{t^2-7}{6}\)
Phương trình trở thành:
\(-\dfrac{t^2-7}{6}+t=0\)
\(\Leftrightarrow t^2-6t-7=0\Rightarrow\left[{}\begin{matrix}t=-1\left(loại\right)\\t=7\end{matrix}\right.\)
\(\Rightarrow\sqrt{6x^2-12x+7}=7\)
\(\Rightarrow6x^2-12x+7=49\)
\(\Rightarrow6x^2-12x-42=0\) (casio)
\(PT\Leftrightarrow\sqrt{6x^2-12x+7}+1-\left(x^2-2x+1\right)=0\\ \Leftrightarrow\dfrac{6x^2-12x+6}{\sqrt{6x^2-12x+7}-1}-\left(x-1\right)^2=0\\ \Leftrightarrow\left(x-1\right)^2\left(\dfrac{6}{\sqrt{6x^2-12x+7}-1}-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\\sqrt{6x^2-12x+7}-1=6\left(1\right)\end{matrix}\right.\\ \left(1\right)\Leftrightarrow\sqrt{6x^2-12x+7}=7\\ \Leftrightarrow6x^2-12x-42=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1-2\sqrt{2}\\x=1+2\sqrt{2}\end{matrix}\right.\)
Thay x=1 ta thấy PT ko thỏa mãn
Thay \(x=1\pm2\sqrt{2}\) ta thấy PT thỏa mãn
Vậy PT có nghiệm \(x=1\pm2\sqrt{2}\)