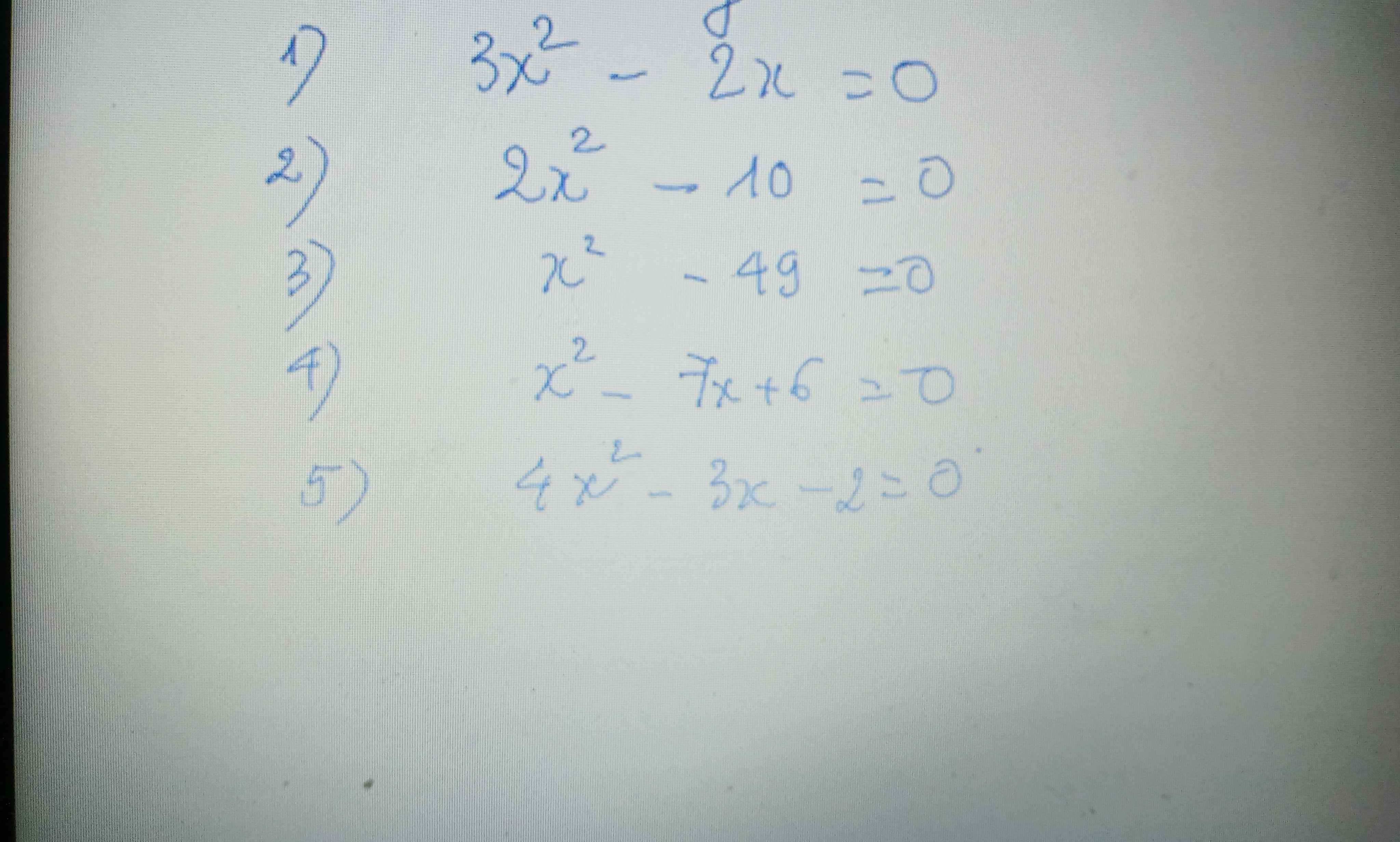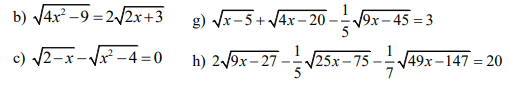ĐKXĐ: \(x\ge-1,x^2+3x+1\ge0\)
\(\sqrt{x^2+3x+1}=\sqrt{x+1}\Rightarrow x^2+3x+1=x+1\)
\(\Rightarrow x^2+2x=0\Rightarrow x\left(x+2\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
Thử lại thấy \(x=0\) là nghiệm
ĐK: x ≥ -1
Bình phương 2 vế, ta đc:
\(x^2+3x+1=x+1\)
⇔ \(x^2+\text{2}x=0\)
⇔ \(x\left(x+2\right)=0\)
⇒ \(\left[{}\begin{matrix}x=0\\x+2=0\end{matrix}\right.\) ⇔ \(\left[{}\begin{matrix}x=0\left(TM\right)\\x=-2\left(KTM\right)\end{matrix}\right.\)
Vậy x = 0
ĐKXĐ: \(x\ge-1\)
Ta có: \(\sqrt{x^2+3x+1}=\sqrt{x+1}\)
\(\Leftrightarrow x^2+3x+1=x+1\)
\(\Leftrightarrow x^2+2x=0\)
\(\Leftrightarrow x\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(nhận\right)\\x=-2\left(loại\right)\end{matrix}\right.\)
Vậy: S={0}