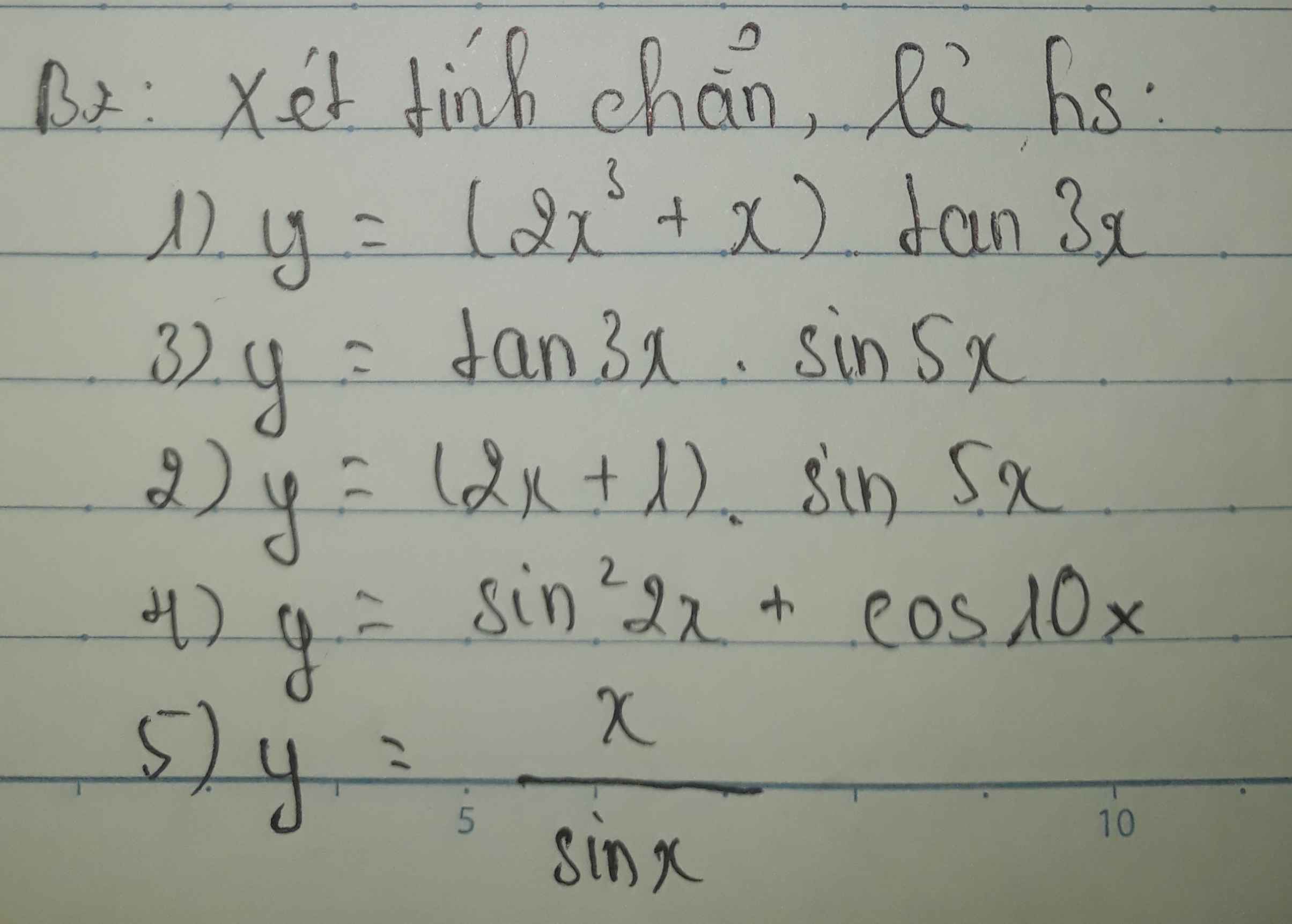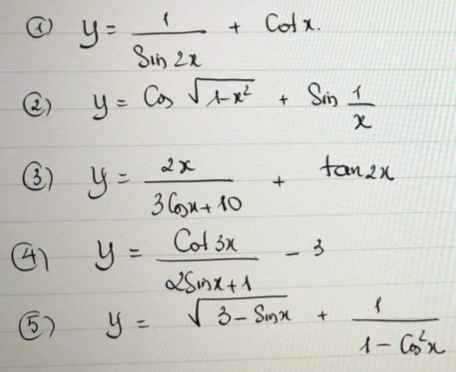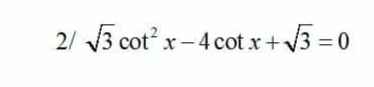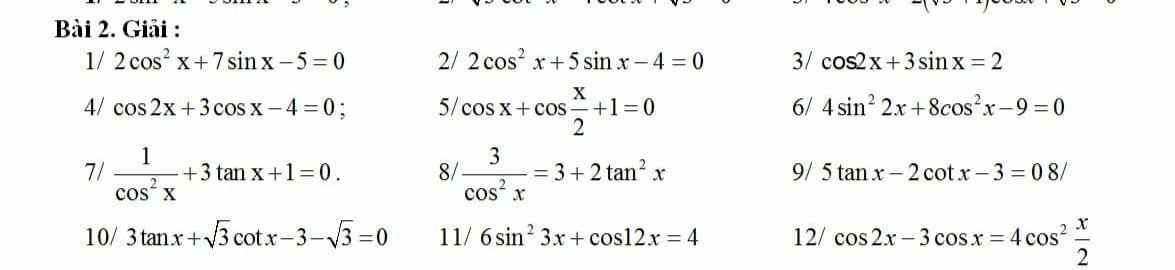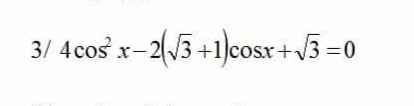Tất cả \(k\in Z\)
1.
a. \(\Leftrightarrow\dfrac{1}{2}sinx+\dfrac{\sqrt{3}}{2}cosx=1\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{3}\right)=1\)
\(\Leftrightarrow x+\dfrac{\pi}{3}=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+k2\pi\)
Đáp án trong đề bị sai
b.
\(\Leftrightarrow\dfrac{1}{2}cos7x-\dfrac{\sqrt{3}}{2}sin7x=-\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow cos\left(7x+\dfrac{\pi}{3}\right)=cos\left(\dfrac{3\pi}{4}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}7x+\dfrac{\pi}{3}=\dfrac{3\pi}{4}+k2\pi\\7x+\dfrac{\pi}{3}=-\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}7x=\dfrac{5\pi}{12}+k2\pi\\7x=-\dfrac{13\pi}{12}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5\pi}{84}+\dfrac{k2\pi}{7}\\x=-\dfrac{13\pi}{84}+\dfrac{k2\pi}{7}\end{matrix}\right.\)
Do \(\dfrac{2\pi}{5}\le x\le\dfrac{6\pi}{7}\Rightarrow\left[{}\begin{matrix}\dfrac{2\pi}{5}\le\dfrac{5\pi}{84}+\dfrac{k2\pi}{7}\le\dfrac{6\pi}{7}\\\dfrac{2\pi}{5}\le-\dfrac{13\pi}{84}+\dfrac{k2\pi}{7}\le\dfrac{6\pi}{7}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\dfrac{143}{120}\le k\le\dfrac{67}{24}\\\dfrac{233}{120}\le k\le\dfrac{85}{24}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}k=1\\k=\left\{2;3\right\}\end{matrix}\right.\)
\(\Rightarrow x=\left\{\dfrac{53\pi}{84};\dfrac{5\pi}{12};\dfrac{59\pi}{84}\right\}\)
e.
\(\Leftrightarrow\dfrac{\sqrt{3}-1}{2\sqrt{2}}sinx+\dfrac{\sqrt{3}+1}{2\sqrt{2}}cosx=sin2x\)
\(\Leftrightarrow sinx.cos\left(\dfrac{5\pi}{12}\right)+cosx.sin\left(\dfrac{5\pi}{12}\right)=sin2x\)
\(\Leftrightarrow sin\left(x+\dfrac{5\pi}{12}\right)=sin2x\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=x+\dfrac{5\pi}{12}+k2\pi\\2x=\dfrac{7\pi}{12}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5\pi}{12}+k2\pi\\3x=\dfrac{7\pi}{12}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5\pi}{12}+k2\pi\\x=\dfrac{7\pi}{36}+\dfrac{k2\pi}{3}\end{matrix}\right.\)
f.
\(\Leftrightarrow sin8x-\sqrt{3}cos8x=\sqrt{3}sin6x+cos6x\)
\(\Leftrightarrow\dfrac{1}{2}sin8x-\dfrac{\sqrt{3}}{2}cos8x=\dfrac{\sqrt{3}}{2}sin6x+\dfrac{1}{2}cos6x\)
\(\Leftrightarrow sin\left(8x-\dfrac{\pi}{3}\right)=sin\left(6x+\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}8x-\dfrac{\pi}{3}=6x+\dfrac{\pi}{6}+k2\pi\\8x-\dfrac{\pi}{3}=\dfrac{5\pi}{6}-6x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{2}+k2\pi\\14x=\dfrac{7\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=\dfrac{\pi}{12}+\dfrac{k\pi}{7}\end{matrix}\right.\)
2.
Theo điều kiện có nghiệm của pt bậc nhất, pt có nghiệm khi:
\(m^2+\left(m+1\right)^2\ge\left(m+2\right)^2\)
\(\Leftrightarrow m^2-2m-3\ge0\)
\(\Rightarrow\left[{}\begin{matrix}m\ge3\\m\le-1\end{matrix}\right.\)
3.
\(\Leftrightarrow2y+y.sinx+y.cosx=2cosx-sinx+1\)
\(\Leftrightarrow\left(y+1\right)sinx+\left(y-2\right)cosx=1-2y\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất
\(\Rightarrow\left(y+1\right)^2+\left(y-2\right)^2\ge\left(1-2y\right)^2\)
\(\Leftrightarrow y^2-y-2\le0\)
\(\Rightarrow-1\le y\le2\)
\(y_{min}=-1\) ; \(y_{max}=2\)
c.
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}sinx+\dfrac{1}{2}cosx=-cos3x\)
\(\Leftrightarrow cos\left(x-\dfrac{\pi}{3}\right)=cos\left(\pi+3x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}\pi+3x=x-\dfrac{\pi}{3}+k2\pi\\\pi+3x=-x+\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=-\dfrac{4\pi}{3}+k2\pi\\4x=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{2\pi}{3}+k\pi\\x=-\dfrac{\pi}{6}+\dfrac{k\pi}{2}\end{matrix}\right.\)
\(\Leftrightarrow x=-\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)
d.
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}cos5x+\dfrac{1}{2}sin5x=-sin17x\)
\(\Leftrightarrow sin\left(5x+\dfrac{\pi}{3}\right)=sin\left(-17x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}5x+\dfrac{\pi}{3}=-17x+k2\pi\\5x+\dfrac{\pi}{3}=\pi+17x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}22x=-\dfrac{\pi}{3}+k2\pi\\12x=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{66}+\dfrac{k\pi}{11}\\x=-\dfrac{\pi}{18}+\dfrac{k\pi}{6}\end{matrix}\right.\)
g.
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}cos2x+\dfrac{1}{2}sin2x+sin\left(2x-\dfrac{\pi}{6}\right)=\sqrt{2}\)
\(\Leftrightarrow cos\left(2x-\dfrac{\pi}{6}\right)+sin\left(2x-\dfrac{\pi}{6}\right)=\sqrt{2}\)
\(\Leftrightarrow\sqrt{2}sin\left(2x-\dfrac{\pi}{6}+\dfrac{\pi}{4}\right)=\sqrt{2}\)
\(\Leftrightarrow sin\left(2x+\dfrac{\pi}{12}\right)=1\)
\(\Leftrightarrow2x+\dfrac{\pi}{12}=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow2x=\dfrac{5\pi}{12}+k2\pi\)
\(\Leftrightarrow x=\dfrac{5\pi}{24}+k\pi\)