Giải giúp mình bài này nha, đang cần gấp lắm
Bài 5:
Ta có: \(\dfrac{a+b}{c+b}=\dfrac{a}{c}\)
\(\Rightarrow\left(a+b\right)c=\left(c+b\right)a\)
\(\Rightarrow ac+bc=ac+ab\)
\(\Rightarrow bc=ab\)
\(\Rightarrow\dfrac{c}{a}=\dfrac{b}{b}=1\)
Vậy \(\dfrac{c}{a}=1\) khi \(\left[{}\begin{matrix}a,c\ne0\\c+b\ne0\\b\ne0\end{matrix}\right.\).
Chẳng biết mk nhìn có đúng không nhưng chữ bạn khó nhìn quá.
Ta có:
\(\dfrac{a+b}{c+b}=\dfrac{a}{c}\\ \Rightarrow\left(a+b\right).c=\left(c+b\right).a\\ \Rightarrow ac+bc=ac+ab\\ bc-ab=ac-ac\\ b\left(c-a\right)=0\)
\(\Rightarrow b=0\) hoặc \(c-a=0\)
Vì theo bài ra: \(b\ne0\) nên:
\(\Rightarrow c-a=0\\ \Rightarrow c=a\)
Thay \(c=a\) vào \(\dfrac{a+b}{c+b}=\dfrac{a}{c}\), ta có:
\(\dfrac{c+b}{c+b}=\dfrac{c}{a}\\ \Rightarrow\dfrac{c}{a}=1\)
Vậy: \(\dfrac{c}{a}=1\)
---
Chúc bạn học tốt :)
theo bài ra ta có:
\(\dfrac{a+b}{c+b}=\dfrac{a}{c}\)
=> (a + b)c = (c + b)a
=> ac + bc = ac + ab
=> bc = ab
=> c = a
vậy \(\dfrac{c}{a}=1\)
cái này tui biết kết quả thui , chắc đúng luôn .
c / a = 1
Giúp tớ nha mn, đang cần gấp lắm. Ai giải hết tick liền luôn nha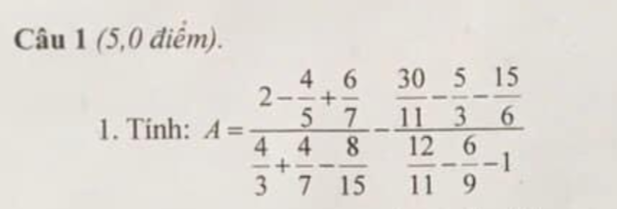
Mình đang cần gấp lắm
Mình đang cần gấp lắm ạ