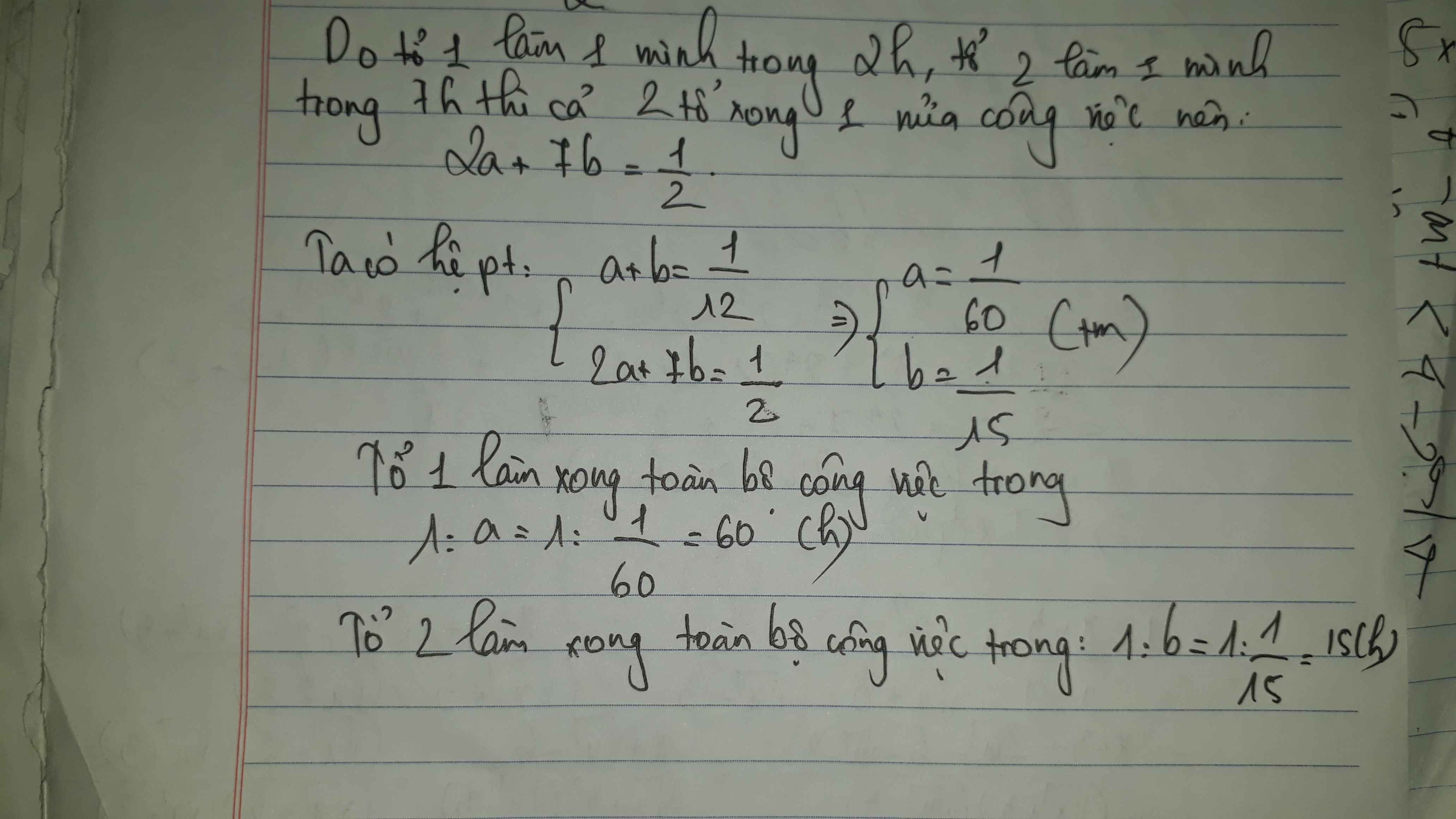Gọi thời gian tổ 1 hoàn thành công việc khi làm một mình là x(giờ)
thời gian tổ 2 hoàn thành công việc khi làm một mình là y(giờ)
(Điều kiện: x>12; y>12)
Trong 1 giờ, tổ 1 làm được: \(\dfrac{1}{x}\)(công việc)
Trong 1 giờ, tổ 2 làm được: \(\dfrac{1}{y}\)(công việc)
Trong 1 giờ, hai tổ làm được: \(\dfrac{1}{12}\)(công việc)
Do đó, ta có phương trình: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\)(1)
Vì khi tổ 1 làm một mình trong 2 giờ và tổ 2 làm một mình trong 7 giờ thi hai tổ làm được một nửa công việc nên ta có phương trình:
\(\dfrac{2}{x}+\dfrac{7}{y}=\dfrac{1}{2}\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\\\dfrac{2}{x}+\dfrac{7}{y}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{2}{y}=\dfrac{1}{6}\\\dfrac{2}{x}+\dfrac{7}{y}=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-5}{y}=\dfrac{-1}{3}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=15\\\dfrac{1}{x}=\dfrac{1}{12}-\dfrac{1}{15}=\dfrac{1}{60}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=60\\y=15\end{matrix}\right.\)(thỏa ĐK)
Vậy: Tổ 1 cần 60 giờ để hoàn thành công việc khi làm một mình
Tổ 2 cần 15 giờ để hoàn thành công việc khi làm một mình