ĐỊNH LÝ LÁ CỜ ANH. (Cuộc thi Trí tuệ VICE - Bài viết | Facebook)
Cho một điểm P nằm trên mặt phẳng hình chữ nhất ABCD, khi đó tổng diện tích hai hình vuông với độ dài cạnh lần lượt là khoảng cách từ điểm P đến hai đỉnh đối nhau bằng tổng diện tích hai hình vuông với các cạnh lần lượt là khoảng cách từ điểm P đến hai đỉnh đối còn lại.

| Cho tam giác ABC có AD = 1 3 AC, BE = 1 2 BD. Diện tích tam giác EBC là 12cm2. a) Tính diện tích tam giác DBC. b) Tính diện tích tam giác ABC |
Because Margaret’s mother was sick, she stayed at home
1 hình chữ nhật có 2 lần chiều rộng hơn chiều dài 5m nhưng 2 lần chiều dài lại hơn chiều rộng 10m tính chu vi hình chữ nhật đố!
cho hình bên ABC=40 ,FBH=140
chứng minh CD bằng EF
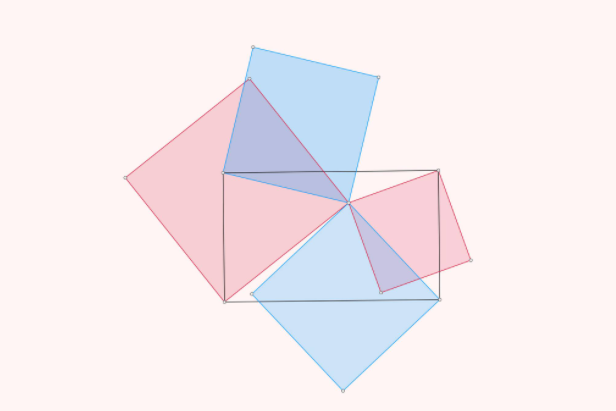
Theo đề thì bài toán trở thành: PD^2 + PB^2 = PA^2 + PC^2
Kẻ PE⊥AB, PF⊥BC, PG⊥CD, PH⊥DA
Khi đó, theo định lí Pythagore: PD² = PH² + DH²; PB² = PE² + BE²; PA² = PE² + AE²; PC² = PF² + CF²
Suy ra: PD² + PB² = PH² + DH² + PE² + BE² = PE² + AE² + PF² + CF² = PA² + PC²
Vậy bài toán được chứng minh.
Chứng minh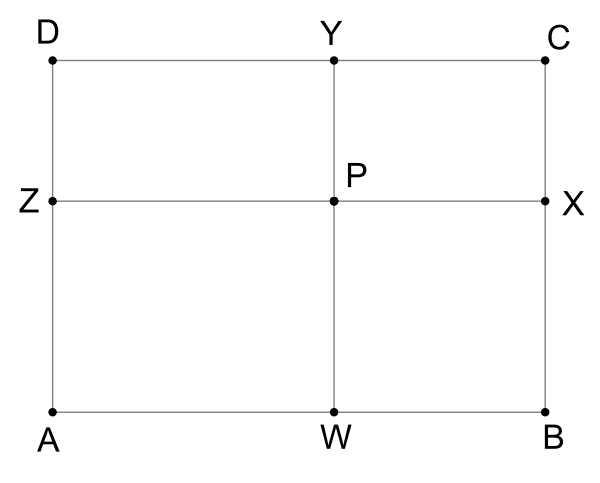 Minh hoạ cách chứng minh
Minh hoạ cách chứng minh
Hình chiếu của P tới các cạnh AB, BC, CD, và AD lần lượt là các điểm w, x, y và z. Khi đó wxyz là một tứ giác có hai đường chéo vuông góc
Áp dụng định lý Pytago cho tam giác vuông AwP, và ta thấy wP = Az, do đó
tương tự ta có:

Do đó: 
tick cho mik nha
Hình chiếu của P tới các cạnh AB, BC, CD, và AD lần lượt là các điểm w, x, y và z. Khi đó wxyz là một tứ giác có hai đường chéo vuông góc
Áp dụng định lý Pytago cho tam giác vuông AwP, và ta thấy wP = Az, do đó
tương tự ta có:
vàDo đó:

















