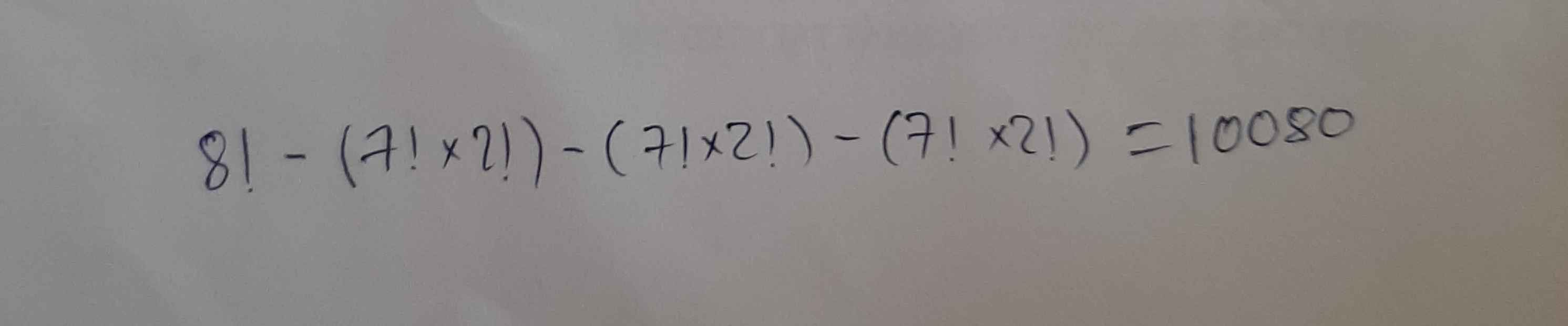Cho mình hỏi, sao cách này lại sai. Ý tưởng của mình là 8 số lặp trừ đi cặp số đứng gần
Chỉ ra cách sai rồi giải theo ý tưởng hóa vị được không mn ới, help me
Sai lầm ở rất nhiều chỗ chứ ko phải 1 chỗ:
Đầu tiên, xếp 8 kí tự này theo thứ tự bất kì: có \(\dfrac{8!}{2!.2!.2!}=5040\) cách chứ ko phải \(8!\) cách
(Do có 3 kí tự lặp lại 2 lần là A,H,N nên phải dùng hoán vị lặp)
8 kí tự gồm 2 chữ A, 2 chữ H, 2 chữ N, 1 chữ T, 1 chữ M
- Chọn ra 1 cặp từ 3 cặp: \(C_3^1=3\) cách
Coi 1 cặp là 1 kí tự, hoán vị nó với 6 kí tự còn lại (trong đó có 2 kí tự lặp 2 lần)
\(\dfrac{7!}{2!.2!}=1260\) cách
\(\Rightarrow3.1260=3780\) cách chọn ra 1 cặp đứng cạnh nhau (trường hợp này bao hàm trường hợp dưới)
- Chọn ra 2 cặp cạnh nhau từ 3 cặp: \(C_3^2=3\) cách
Coi 2 cặp là 2 kí tự, hoán vị với 4 kí tự còn lại (trong đó có 1 kí tự lặp 2 lần):
\(\dfrac{6!}{2!}=360\) cách
\(\Rightarrow3.360=1080\) cách (trường hợp này bao hàm trường hợp dưới)
- Chọn ra 3 cặp cạnh nhau: 1 cách
Coi 3 cặp là 3 kí tự, hoán vị nó với 2 kí tự còn lại: \(5!=120\) cách
\(\Rightarrow1.120=120\) cách
Số cách chọn ít nhất 1 kí tự giống nhau đứng cạnh nhau:
\(3780-\left(1080-3.120\right)+120=3180\) cách
Số cách thỏa mãn yêu cầu đề bài:
\(5040-3180=1860\) cách
Bài toán khá dễ, nhưng là dễ sợ, nếu ko quen thuộc với việc cộng trừ loại trùng lặp dựa trên biểu đồ Ven thì quỳ gối đấy :D
Gọi số đó là \(\overline{abcde1}\)
Bộ bcde mỗi số có 10 cách chọn
Gọi số dư của \(b+c+d+e+1\) khi chia cho 9 là k
- Nếu \(k=0\Rightarrow a=9\) có 1 cách chọn
- Nếu \(k=1\Rightarrow a=8\) có 1 cách chọn
Tương tự, k=2, a=7; k=3; a=6;...; k=8; a=1
Có nghĩa là với mỗi giá trị k luôn có đúng 1 cách chọn a
Do đó số số thỏa mãn là: \(10^4=10000\) số
//Làm kiểu lớp 6:
Số nhỏ nhất có 6 chữ số chia hết cho 9 là \(100071\)
Gọi k là số số có 6 chữ số tận cùng bằng 1 chia hết cho 9
\(\Rightarrow100071+90\left(k-1\right)\le999999\)
\(\Rightarrow k\le10000,2\Rightarrow k=10000\)