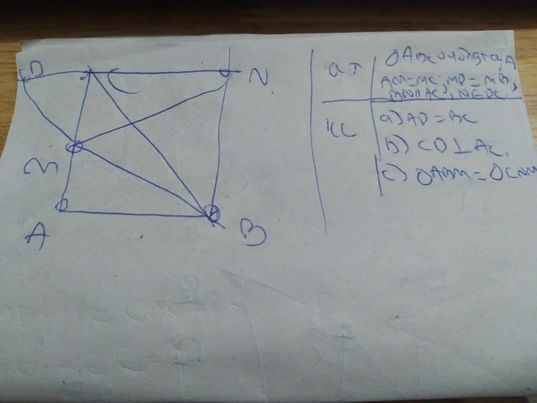
a: Xét ΔAMD và ΔCMB có
MA=MC
\(\widehat{AMD}=\widehat{CMB}\)
MD=MB
Do đó: ΔAMD=ΔCMB
=>AD=BC
b: Xét ΔMAB và ΔMCD có
MA=MC
\(\widehat{AMB}=\widehat{CMD}\)
MB=MD
Do đó: ΔMAB=ΔMCD
=>\(\widehat{MAB}=\widehat{MCD}=90^0\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
=>CD\(\perp\)AC
c: Xét tứ giác ABNC có
AB//NC
AC//BN
Do đó: ABNC là hình bình hành
=>CN=AB
Xét ΔMAB vuông tại A và ΔMCN vuông tại C có
MA=MC
AB=CN
Do đó: ΔMAB=ΔMCN
Đúng 1
Bình luận (0)

