Hình nón có đường sinh \(l=6a\) và đáy là đường tròn ngoại tiếp tam giác đều cạnh 6a
\(\Rightarrow r=\dfrac{cạnh.\sqrt{3}}{3}=\dfrac{6a.\sqrt{3}}{3}=2a\sqrt{3}\)
\(\Rightarrow S_{xq}=\pi rl=12\sqrt{3}\pi a^2\)
Hình nón có đường sinh \(l=6a\) và đáy là đường tròn ngoại tiếp tam giác đều cạnh 6a
\(\Rightarrow r=\dfrac{cạnh.\sqrt{3}}{3}=\dfrac{6a.\sqrt{3}}{3}=2a\sqrt{3}\)
\(\Rightarrow S_{xq}=\pi rl=12\sqrt{3}\pi a^2\)
Câu 1 : Mặt cầu (S) có bán kính R = \(a\sqrt{2}\) . Tính diện tích của mặt cầu (S)
A. \(8a^2\) B. \(4\Pi a^2\) C. \(8\Pi a^2\) D. \(16\Pi a^2\)
Câu 2 : Công thức tính thể tích khối cầu có bán kính R ?
A. \(\frac{4}{3}\Pi R^2\) B. \(\frac{4}{3}\Pi R^3\) C. \(\frac{1}{3}\Pi R^3\) D. \(\Pi R^3\)
Câu 3 : Một hình hộp chữ nhật có ba kích thước tương ứng là a , 2a , 2a . Tính thể tích khối cầu ngoại tiếp hình hộp
A. \(\frac{9\Pi a^3}{5}\) B. \(\frac{9\Pi a^3}{4}\) C. \(9\Pi a^3\) D. \(\frac{9\Pi a^3}{2}\)
Câu 4 : Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a , AD = \(a\sqrt{3}\) . Cạnh bên SA vuông góc với đáy và SC tạo với đáy 1 góc 600 . Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABCD
A. Tâm là trung điểm SC , R = 2a
B. Tâm là trung điểm SC , R = 4a
C. Tâm trùng với tâm của đáy , R = a
D. Tâm là trung điểm SD , R = \(\frac{a\sqrt{15}}{2}\)
Câu 5 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với đáy , cạnh bên SB bằng \(a\sqrt{3}\) . Tính thể tích khối cầu ngoại tiếp S.ABCD
A. \(\frac{4}{3}\Pi a^3\) B. \(\frac{16\sqrt{2}}{3}a^3\) C. \(12\sqrt{3}a^3\) D. \(\frac{4}{3}a^3\)
HELP ME !!!!!!!!!!!!!
Câu 1 : Cho hình chóp có các cạnh bên bằng nhau và bằng a , độ dài đường cao bằng h . Tính bán kính mặt cầu ngoại tiếp hình chóp đã cho .
A. R = \(\frac{a^2}{2h}\) B. R = \(\frac{2a^2}{h}\) C. R = \(\frac{2h^2}{a}\) D. R = \(\frac{h^2}{2a}\)
Câu 2 : Cho hình chóp S.ABCD có cạnh đáy a , cạnh bên bằng \(\frac{a\sqrt{3}}{2}\) . Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD
A. \(\frac{3a}{2}\) B. \(\frac{a}{2}\) C. a D. \(\frac{3a}{4}\)
Câu 3 : Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB = \(a\sqrt{2}\) , SA = SB = SC . Góc giữa SA và (ABC) bằng 600 . Tính diện tích mặt cầu ngoại tiếp S.ABC
A. \(\frac{16\Pi a^2}{9}\) B. \(\frac{16\Pi a^2}{3}\) C. \(4\Pi a^2\) D. \(\frac{64\Pi a^2}{3}\)
Câu 4 : Cho mặt cầu (S) có bán kính R = \(\sqrt{3}\) . Xét các điểm A ,B , C , D nằm trên mặt cầu (S) sao cho AB , AC , AD đôi một vuông góc với nhau . Thể tích khối tứ diện ABCD có giá trị lớn nhất bằng
A. \(\frac{8}{3}\) B. 8 C. 4 D. \(\frac{4}{3}\)
help me !!!!!!
Cho tứ diện ABCD có \(AB=\dfrac{a\sqrt{3}}{2}\) và các cạnh còn lại đều bằng \(a\) . Biết rằng bán kính mặt cầu ngoại tiếp tứ diện ABCD bằng \(\dfrac{a\sqrt{m}}{n}\) với \(m,n\in N\)*; \(m\le15\). Tổng \(T=m+n\) bằng?
A. 15 B. 17 C. 19 D. 21
Có gì cho mình xin công thức chung để tính bán kính mặt cầu ngoại tiếp tứ diện luôn ạ, mình cảm ơn nhiều♥
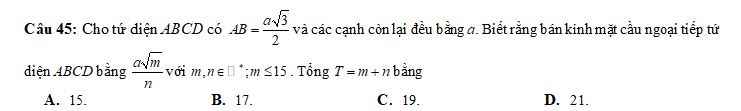
Diện tích xung quanh của hình nón có bán kính đáy bằng a và chiều cao a√3 là:
A. 2√3πa^2
B.πa^2
C.√2πa^2
D.√3πa^2
Trong không gian cho tam giác ABC vuông tại A. Quay tam giác ABC xung quanh cạnh AB, ta thu được một hình nón. Tính diện tích toàn phần của hình nón thu được biết rằng AC =a; góc ACB=60°:
A. √3πa^2
B. πa^2
C. 2√3πa^2
D. 2πa^2
1)Cho khối lập phương có độ dài đường chéo bằng \(\sqrt{3}\)cm. Tính thể tích khối lập phương đó
2) Cho hình khối lăng trụ tam giác ABC.A'B'C' có thể tích bằng 1. TÍnh thể tích khối chóp A'.ABC' theo V
3)Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tamiacs đều cạnh a và đường thẳng A'C tạo với mặt phẳng (ABB'A') một góc 300 . Tính thể tích khối lăng trụ ABC.A'B'C'
4)Cho hình chóp tam giác S.ABC có ASB=CSB=600 , SA=SB=SC=2a. Tính thể tích khối chóp S.ABCD
5) Cho hình chóp S.ABCD có SA vuông góc với (ABCD), SB=\(a\sqrt{5}\), ABCD là hình thoi cạnh a, góc ABC = 600 . Tính thể tích khối chóp S.ABCD
cắt một hình nón bằng một mặt phẳng đi qua trục của nó, ta được thiết diện là một tam giác đều cạnh \(2a\sqrt{2}\) . Diện tích xung quanh của khối nón là:
Giúp mình câu hỏi này với ạ.
Đề bài: Khi sản xuất vỏ lon sữa Ông Thọ hình trụ, nhà sản xuất luôn đặt tiêu chí sao cho chi phí sản xuất vỏ lon là nhỏ nhất, tức nguyên liệu được dùng là ít nhất. Hỏi khi đó tổng diện tích toàn phần của lon sữa là bao nhiêu khi nhà sản xuất muốn thể tích của hộp là \(Vcm^3\).
Các đáp án lựa chọn là:
\(A.S_{tp}=6\sqrt[3]{\dfrac{\pi V^2}{4}}\) \(B.S_{tp}=3\sqrt[]{\dfrac{\pi V^2}{4}}\) \(C.S_{tp}=3\sqrt[3]{\dfrac{\pi V^2}{4}}\) \(D.S_{tp}=6\sqrt[]{\dfrac{\pi V^2}{4}}\)
1. Diện tích toàn phần của hình nón có khoảng cách từ tâm của đáy đến đường sinh bằng \(\sqrt{3}\). Thiết diện qua trục tam giác đều là??
2.Cho hình nón tam giác đều S.ABC có cạnh đáy bằng a và góc giữa cạnh bên và đáy bằng 60 độ , diện tính xung quanh của hình nón đinh S và đáy là hình tròn ngoại tiếp??
3. Thiết diện qua trục của một tam giác vuông cân có cạnh góc vuông bằng a. Một thiết diện qua đỉnh tạo với đáy một góc 60 độ. Diện tích của thiết diện bằng??
1)cho tứ diện đều ABCD có cạnh bằng a. Tính diện tích xung quanh của hình trụ có đáy là đường tròn ngoại tiếp tam giác BCD và có chiều cao bằng chiều cao của tứ diện
2) Cho hình trụ có hai đường tròn đáy là (O,R) và (O', R'), OO'= h. Biết AB là một đường kính của đường tròn (O,R). Biết rằng tam giác O'AB đều. Tỉ số h/R bằng