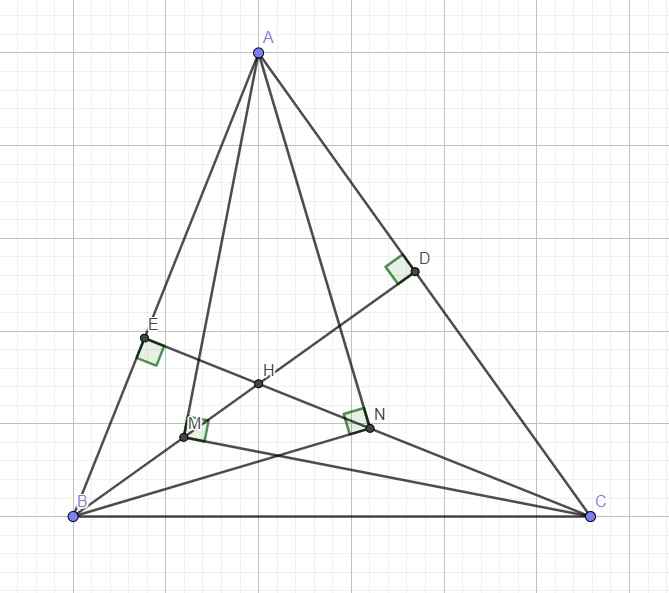
1.
Tam giác AMC vuông tại M với đường cao MD
Áp dụng hệ thức lượng: \(AM^2=AD.AC\) (1)
Tương tự ta có:
\(AN^2=AE.AB\) (2)
Mặt khác xét hai tam giác vuông ABD và ACE có:
\(\widehat{BAC}\) chung
\(\Rightarrow\Delta_VABD\sim\Delta_VACE\) (g.g)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{AD}{AE}\) \(\Leftrightarrow AB.AE=AC.AD\) (3)
(1);(2);(3) \(\Rightarrow AM^2=AN^2\) \(\Rightarrow AM=AN\)
Bài 2 tham khảo tại đây:
Cho tam giác ABC vuông tại A , đường cao AH . Biết AB/AC = 20/21 , AH = 420 . Tính chu vi tam giác ABC - Hoc24