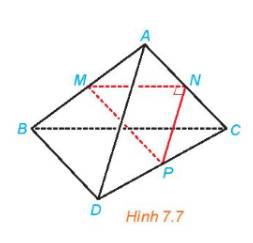
+) Xét tam giác ABC có
M, N lần lượt là trung điểm của AB, AC
\( \Rightarrow \) MN là đường trung bình của tam giác ABC
\( \Rightarrow \) MN // BC
Mà NP \( \bot \) MN nên NP \( \bot \) BC
Xét tam giác ADC có
N, P lần lượt là trung điểm của AC, CD
\( \Rightarrow \) PN là đường trung bình của tam giác ADC
\( \Rightarrow \) PN // AD
Mà NP \( \bot \) BC nên AD \( \bot \) BC
+) BC // MN mà \(MN \subset \left( {MNP} \right) \Rightarrow BC//\left( {MNP} \right)\)
PN // AD mà \(PN \subset \left( {MNP} \right) \Rightarrow AD//\left( {MNP} \right)\)
Vậy AD và BC chéo nhau.
Xét ΔABC có AM/AB=AN/AC
nên MN//BC
=>BC vuông góc NP
Xét ΔCAD có CN/CA=CP/CD
nên NP//AD
mà BC vuông góc NP
nên BC vuông góc AD
PN//AD
=>AD//(MNP)
BC//NP
=>BC//(MNP)
=>AD và BC chéo nhau