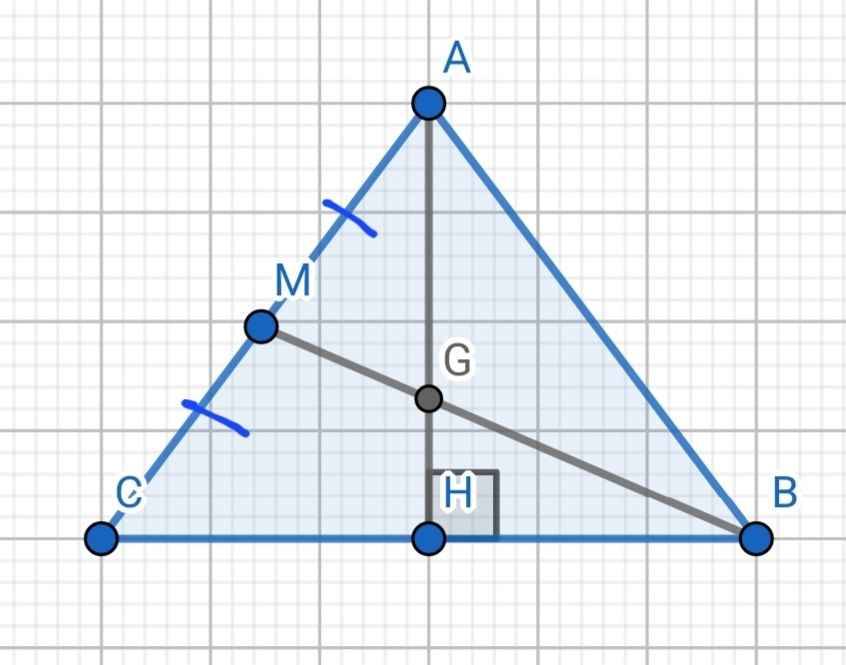
Do ∆ABC cân tại A
AH ⊥ BC (gt)
⇒ AH vừa là đường cao vừa là đường trung tuyến của ∆ABC
Do M là trung điểm AC
⇒ AM là đường trung tuyến của ∆ABC
⇒ G là trọng tâm của ∆ABC
⇒ AG = 2/3 AH = 2/3 . 6 = 4 (cm)

Do ∆ABC cân tại A
AH ⊥ BC (gt)
⇒ AH vừa là đường cao vừa là đường trung tuyến của ∆ABC
Do M là trung điểm AC
⇒ AM là đường trung tuyến của ∆ABC
⇒ G là trọng tâm của ∆ABC
⇒ AG = 2/3 AH = 2/3 . 6 = 4 (cm)
Cho tam giác ABC cân tại A. Biết AC=5cm, BC=6cm. Kẻ AH vuông góc với BC tại H a) CMR: Tam giác ABH=tam giác ACH. b) Tính độ dài đoạn thẳng AH c) Từ H kẻ đường thẳng song song với AC, cắt AB tại M. CMR: M là trung điểm của AB
cho tam giác ABC cân tại a ( góc a= 90 độ ) dựng AH vuông góc với BC tại H ( H thuộc BC)
a chứng minh tam giác ABC = tam giác AHC và HB=HC
b với AB =30cm bc =36cm tính độ dài AH
c kẽ đường trung tuyến BM của tam giác ABC cắt AH tại G tính độ dài AG và BM
gấp ạ giúp mình câu c
Cho tam giác ABC cân tại A(góc A nhọn). Vẽ AH vuông góc với BC (H thuộc BC). a. Chứng minh tam giác AHB bằng tam giác AHC b. Đường thẳng qua H song song với AB cắt AC tại D. Gọi M là trung điểm của HC. Chứng minh tam giác DHC cân và DM song song với AH.
giúp em câu b
cho tam giác ABC cân tại A. Trên cạnh BC lần lượt là BC lần lượt lấy các điểm M và N ( M nằm giữa B và N ) sao cho BM = CN. Kẻ MH vuông góc với AB; NK vuông góc với AC. Chứng minh:
a) Tam giác MHB = tam giác NKC
b) AH = AK
c) tam giác AMN cân tại A
Cho tam giác ABC cân tại A .Trên tia đối của tia BC lấy điểm M .Trên tia đối của tia BC lấy N.Sao cho BM=CN.Kẻ BH vuông góc với AM,CK vuông góc với AM
a) CM: Tam giác AMN cân tại A
b)CM :BH=CK và AH=AK
c)CM:HB cắt AC tại O .CM AO là tia p/g của góc BAC và AO vuông góc với BC
![]()
![]()
Cho tam giác ABC cân tại A có AB = AC = 10 cm;BC = 12 cm.Kẻ AH vuông góc với BC. a) Chứng minh HB = HC;tính AH. b) kẻ Bx vuông góc với AB tại B; Cy vuông góc với AC tại C; Bx và Cy cắt nhau tại M. chứng minh AM là tia phân giác của góc BAC và suy ra A,H,M thẳng hàng. c)kẻ HK song song với MB(K thuộc MC) Trên tia HM lấy điểm O sao cho OM = 2OH. Chứng minh ba điểm B,O,K thẳng hàng
Cho tam giác ABC cân tại A. AH vuông góc với BC(H € BC)
a) CM HB=HC
b) Trên tia đối BC lấy điểm M. Trên tia đối CB lấy điểm N sao cho BM=CN. Kẻ BH vuông góc với AM tại E, CF vuông góc với AN tại F. Gọi I là giao điểm của EB và FC. CM A, H, I thẳng hàng
Bài 2: Cho ∆ABC cân tại A, AB = 5cm, BC = 6cm. Kẻ AH vuông góc với BC tại H. a. Chứng minh: ∆AHB = ∆AHC. b. Tính AH. c. Gọi I là trung điểm của AC, trên tia đối của tia IH lấy điểm K sao cho IK = IH. Chứng minh: ∆AIH = ∆CIK. d. Chứng minh: AH // KC. e. Tính HI
cảm ơn
Bài 9: Cho tam giác ABC cân tại A. Điểm H là trung điểm của cạnh BC.
a) Chứng minh: . Chứng minh AH vuông góc với BC.
b) Kẻ HM vuông góc với AB tại M, kẻ HN vuong góc với AC tại N. Chứng minh: .
c) Gọi I là giao điểm của MH và AC, gọi K là giao điểm của NH và AB. Chứng minh tam giác AIK cân.