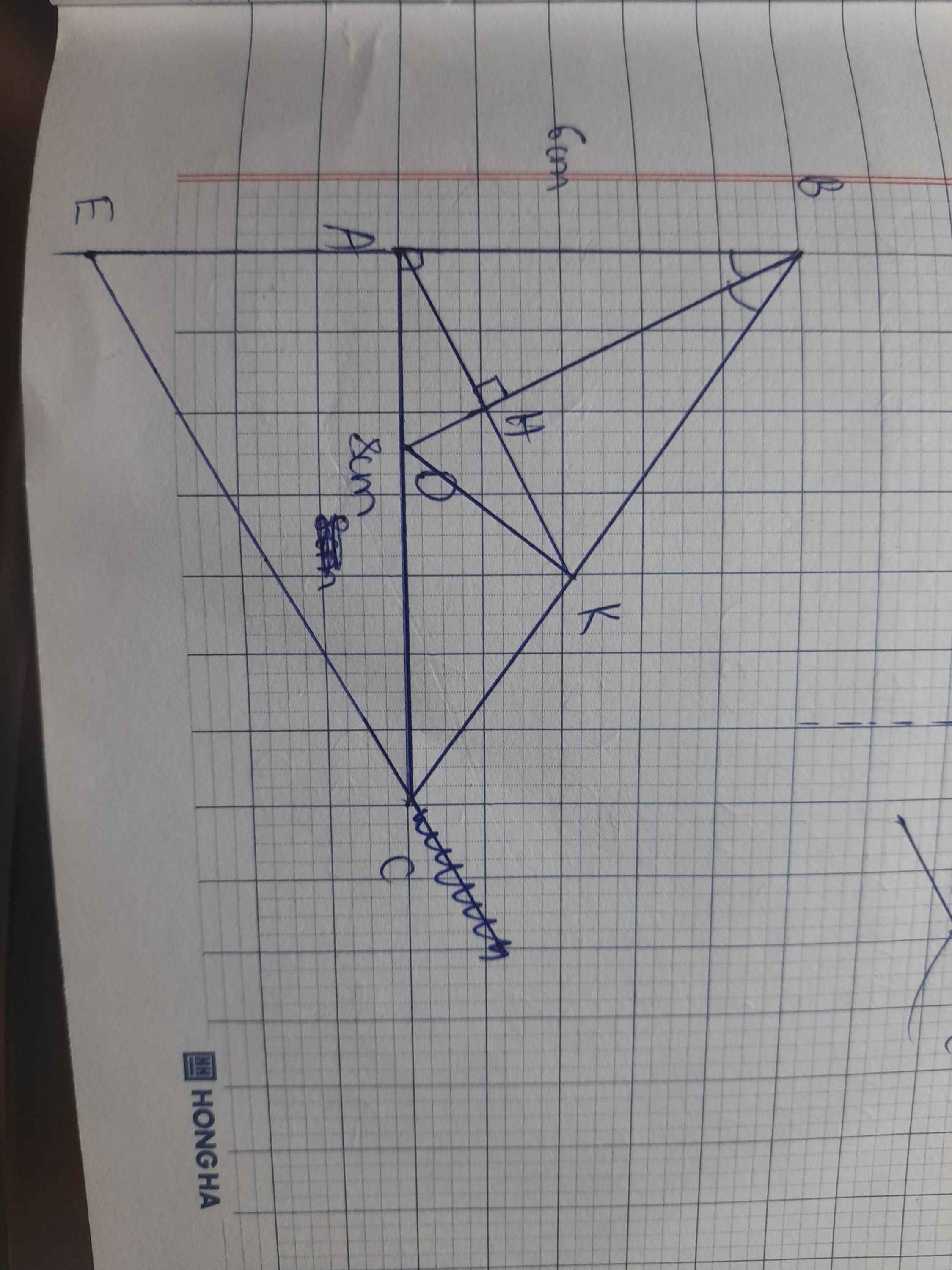
a,
Xét tam giác ABM và tam giác HBM có :
BA = BH ( gt )
BM chung
Góc ABM = góc HBM ( BM là pgiác của góc B )
Suy ra tam giác ABM = tam giác HBM ( cgc) . (1)
b,
Từ (1) suy ra góc BAM = góc BHM = 90 độ ( 2 góc tương ứng ).
Vì góc BHM = 90 độ ( CMT) suy ra MH vuông góc vs BC tại H
c,
Từ ( 1 ) ta lại có MA = MH ( 2 cạnh tương ứng )
Xét tam giác vuông AMK tại A và tam giác vuông HMC tại H có :
- AM = HM ( CMT )
- Góc AMK = góc HMC ( 2 góc đối đỉnh )
Suy ra tam giác AMK = tam giác HMC ( cạnh góc vuông - góc nhọn kề ) . (2)
Từ ( 2 ) suy ra MC = MK ( 2 cạnh tương ứng ) Vì MK = MC ( CMT ) suy ra tam giác KMC cân tại M
d,
Vì BA = BH ( gt ) suy ra tam giác ABH cân tại B .
Vì tam giác ABH cân tại B nên góc BAH = góc BHA = ( 180 độ - góc B )/2 ( 2 góc đáy ). (3)
Tam giác AMK = tam giác HMC ( câu c ) nên AK = HC ( 2 cạnh tương ứng )
Vì BA = BH ( gt ) và AK = HC ( CMT ) suy ra BK = BC
Vì BK = BC suy ra tam giác BKC cân tại B .
Vì tam giác BKC cân tại B suy ra góc K = góc C = ( 180 độ - góc B )/2 . (4)
Từ (3) và (4) suy ra góc BAH = góc BHA = góc K = góc C
Vì góc BAH = góc K ( CMT ) mà 2 góc ở vị trí đồng vị suy ra AH song song với KC.
Hết