a: BC=5cm
\(AH=\dfrac{3\cdot4}{5}=2.4\left(cm\right)\)
\(HB=\dfrac{9}{5}=1.8\left(cm\right)\)
HC=5-1,8=3,2(cm)
b: \(AE\cdot EB+AF\cdot FC\)
\(=HE^2+HF^2\)
\(=FE^2=AH^2\)
Cho tam giác ABC vuông tại A có đường cao AH.
1) Cho biết AB=3 cm, AC=4 cm. Tính độ dài các đoạn BC,HB,HC,AH
2) Vẽ HE vuông góc với AB tại E, HF vuông góc với AC tại F
a) Chứng minh: AE.EB=HE2
b) Chứng minh: AE.EB+AF.FC=AH2
3) Chứng minh: BE=BC. cos3 B
Cho tam giác ABC vuông tại A có đường cao AH. Vẽ HE vuông góc với AB tại E, HF vuông góc với AC tại F.
a) Cho biết AB = 3cm, AC = 4cm. Tính độ dài các đoạn HB, HC, AH
b) Chứng minh: AE.EB + AF.FC = AH2
c) Chứng minh: BE = BC.cos3B
Cho tam giác ABC vuông tại A, có đường cao AH. Vẽ HE vuông góc AB tại E ; vẽ HF vuông góc AC tại F.
Chứng minh: AE.AB=AF.AC
Chứng minh: HB/HC = (AB/AC)2
Cho tam giác ABC vuông tại A, có đường cao AH. Vẽ HE vuông góc AB tại E ; vẽ HF vuông góc AC tại F. Chứng minh: (AE.AB)/(EF.BC) = AF/AB
Bài 3: Cho ∆ ABC vuông tại A, đường cao AH biết HB=4cm ; HC= 9cm . a) Tính AB và AH. b) Từ HE vuông góc với AB, HF vuông góc với AC Tử giác AEHF là hình gì? Tính EF ?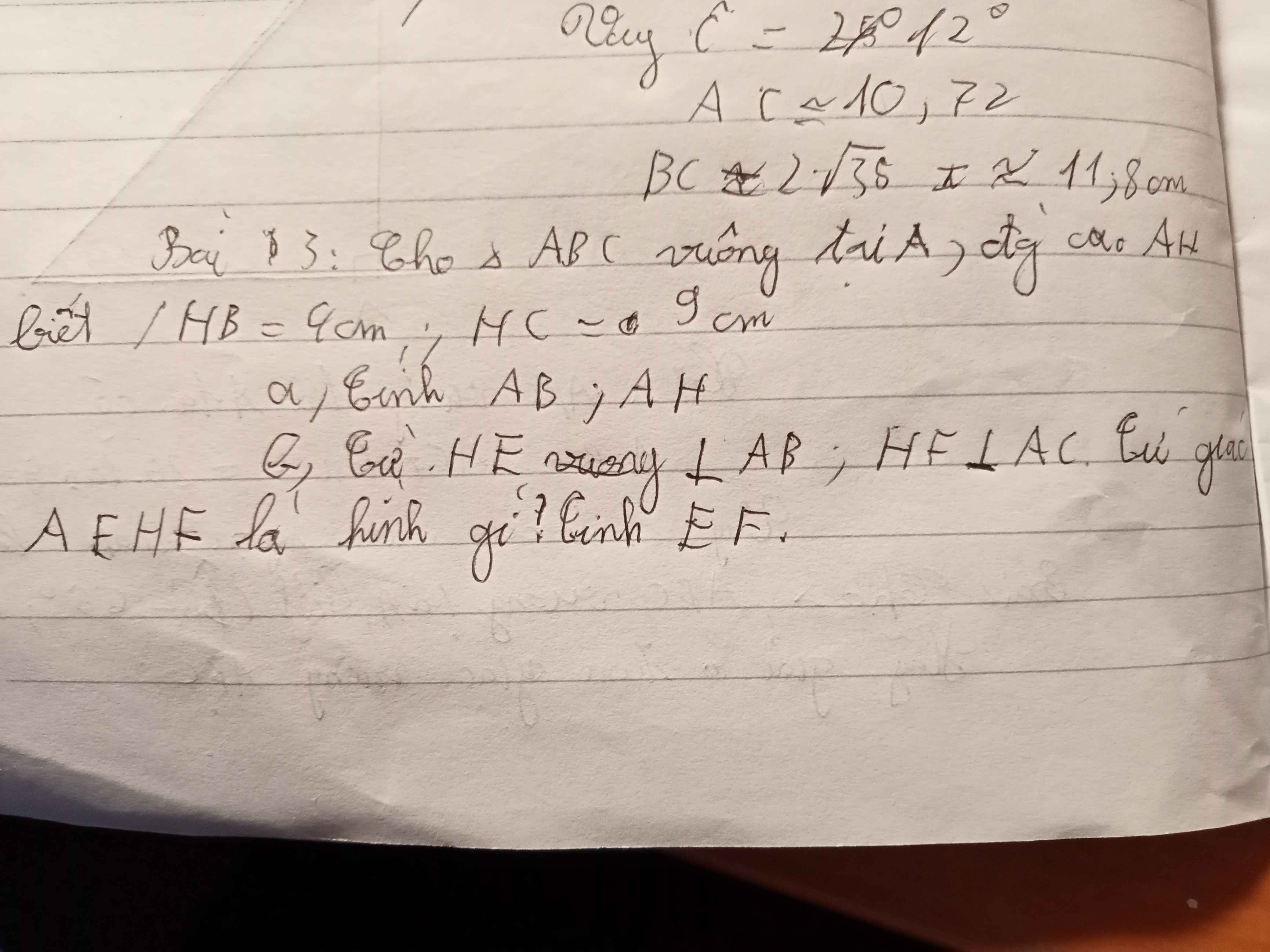
Cho tam giác ABC vuông tại C, đường cao CH. Biết AH = 4cm. HB = 9cm
a) Tính CH, CA ?
b) Kẻ HE vuông góc với AC, F vuông góc với BC (E thuộc AC, F thuộc BC) Chứng minh: CE . CA = CF . CB. Từ đó chứng minh: tam giác CEF đồng dạng với tam giác CBA
c) Chứng minh: AB = ACcosA + BCcosB
Cho tam giác ABC vuông tại A, đường cao AH (HϵBC)
a) Biết AB = 12cm, BC = 20cm. Tính AC, B, AH (góc làm tròn đến độ)
b) Kẻ HE vuông góc AB (EϵAB). Chứng minh: AE.AB=AC2-HC2
c) Kẻ HF vuông góc AC (FϵAC). Chứng minh: AF=AE.tanC
Cho tam giác ABC vuông tại A, đường cao AH, AB=3cm, BC=6cm. 1) Giải tam giác ABC 2) Gọi E, F lần lượt là hình chiếu của H trên cạnh AB và AC. a) Tính độ dài AH và chứng minh: EF=AH b) Tính: EA.EB+AF.FC
Cho tam giác ABC vuông tại A có đường cao AH.
Biết AB = 12 cm, AC = 16 cm.
a) Tính độ dài các đoạn thẳng BC, AH,
BH và CH.
b) Kẻ HE ⊥ AB (E ∈ AB) và HF ⊥ AC
(F ∈ AC). Chứng minh rằng AE.AB =
AF.AC và suy ra tam giác ABC ∼ AFE.
