Gọi D là trung điểm của cạnh AB, ta có:
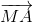 +
+ = 2
= 2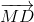
Đẳng thức đã cho trở thành:
2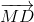 + 2
+ 2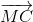 =
= 
=> 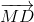 +
+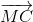 =
= 
Đẳng thức này chứng tỏ M là trung điểm của CD
Gọi D là trung điểm của cạnh AB, ta có:
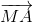 +
+ = 2
= 2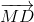
Đẳng thức đã cho trở thành:
2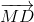 + 2
+ 2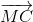 =
= 
=> 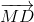 +
+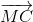 =
= 
Đẳng thức này chứng tỏ M là trung điểm của CD
Cho tam giác ABC
a) Tìm điểm K sao cho \(\overrightarrow{KA}+2\overrightarrow{KB}=\overrightarrow{CB}\)
b) Tìm điểm M sao cho \(\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{0}\)
Cho tam giác ABC. Tìm tập hợp điểm M sao cho: \(\left|\overrightarrow{MA}+\overrightarrow{MB}-2\overrightarrow{MC}\right|=\left|\overrightarrow{MB}+\overrightarrow{MC}\right|\)
Cho ΔABC tìm tập hợp các điểm M thỏa:
a/ \(\left|\overrightarrow{MA}+\overrightarrow{MB}\right|=\left|\overrightarrow{MC}+\overrightarrow{MB}\right|\)
b/ \(\left|2\overrightarrow{MA}+\overrightarrow{MB}\right|=\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|\)
Cho tam giác ABC
a) Xác định M sao cho \(\overrightarrow{MA}+\overrightarrow{MB}+4\cdot\overrightarrow{MC}=0\)
b) Xác định O sao cho \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=2\cdot\overrightarrow{CB}\)
Cho tam giác ABC và một điểm M tùy ý . Chứng minh rằng : \(\overrightarrow{4MA}+\overrightarrow{MB}-5\overrightarrow{MC}=4\overrightarrow{CA}+\overrightarrow{CB}\)
1Cho tam giác ABC và điểm M thõa mãn \(\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{AB}\)
TÌM VỊ TRÍ CỦA M
2 Cho tam giác ABC . Tập hợp điểm M thõa màn
a. \(\left|\overrightarrow{MB}-\overrightarrow{MC}\right|=\left|\overrightarrow{BM}-\overrightarrow{BA}\right|\)
B, VÉC TƠ MA+MB-MC=MD
Cho ΔABC và 3 số thực m,n,p sao co m + n + p ≠ 0. C/m rằng có duy nhất 1 điểm M sao cho \(m\overrightarrow{MA}+n\overrightarrow{MB}+p\overrightarrow{MC}=0\)
Cho tam giác ABC. Tìm tập hợp điểm M sao cho \(\overrightarrow{v}=\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{2MC}cungphuongvoi\overrightarrow{BC}\)
cho tam giác ABC lấy các điểm M,N,P sao cho \(\overrightarrow{MB}-2\overrightarrow{MC}=\overrightarrow{0},\overrightarrow{NA}+\overrightarrow{2NC}=\overrightarrow{0},\overrightarrow{PA}+\overrightarrow{PB}=\overrightarrow{0}\)
a)hãy biểu thị \(\overrightarrow{PM},\overrightarrow{PN}\)theo \(\overrightarrow{AB},\overrightarrow{AC}\)
b)chứng minh M,N,P thẳng hàng