\(\dfrac{AB}{AC}=\dfrac{\sqrt{6}}{3}\Rightarrow AB=\dfrac{AC\sqrt{6}}{3}\)
\(AB.AC=32\sqrt{6}\Rightarrow\dfrac{AC^2\sqrt{6}}{3}=32\sqrt{6}\)
\(\Rightarrow AC^2=96\Rightarrow AC=4\sqrt{6}\)
\(\Rightarrow AB=\dfrac{AC\sqrt{6}}{3}=8\)
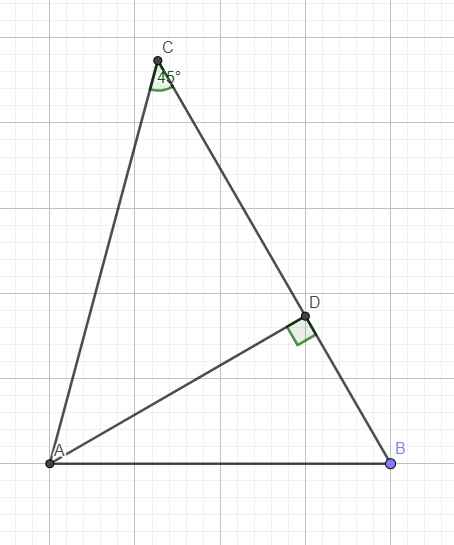
Kẻ đường cao AD ứng với BC
Do \(C=45^0\Rightarrow\widehat{CAD}=90^0-45^0=45^0\Rightarrow\Delta ACD\) vuông cân tại D
\(\Rightarrow AD=CD=\dfrac{AC}{\sqrt{2}}=4\sqrt{3}\)
Pitago tam giác vuông ABD:
\(BD=\sqrt{AB^2-AD^2}=4\)
\(\Rightarrow BC=CD+BD=4+4\sqrt{3}\)
\(cosB=\dfrac{BD}{AB}=\dfrac{4}{8}=\dfrac{1}{2}\Rightarrow B=60^0\)
\(S_{ABC}=\dfrac{1}{2}AD.BC=\dfrac{1}{2}.4\sqrt{3}.\left(4+4\sqrt{3}\right)=...\)