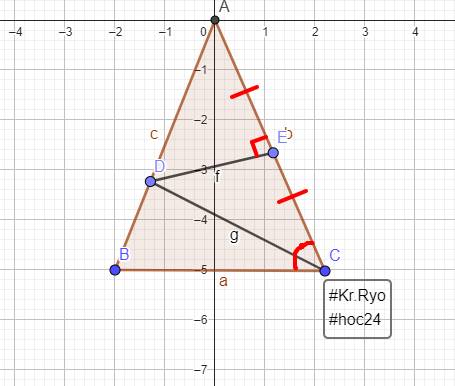
Vì đường trung trực của `AC` cắt `AB` tại `D.`
`@` Theo tính chất của đường trung trực (điểm nằm trên đường trung trực của `1` đoạn thẳng thì cách `2` đầu mút đoạn thẳng đó)
`-> \text {DA = DC}`
Xét `\Delta ACD`: `\text {DA = DC}`
`-> \Delta ACD` cân tại `D.`
`-> \hat {A} = \hat {ACD}` `(1)`
Vì `\text {CD}` là tia phân giác của $\widehat {ACB} (g$$t)$
`->` $\widehat {ACD} = \widehat {BCD} =$ `1/2` $\widehat {ACB}$ `(2)`
Từ `(1)` và `(2)`
`->` $\widehat {ACB} = \widehat {2C_2} = \widehat {2A}$
Mà `\hat {A}=35^0`
`->` $\widehat {ACB}$`=35^0*2=70^0`
Xét `\Delta ABC`:
$\widehat {BAC} + \widehat {ABC}+ \widehat {ACB}=180^0 (\text {định lý tổng 3 góc trong 1 tam giác})$
`-> 35^0+` $\widehat {ABC} + 70^0=180^0$
`->` $\widehat {ABC}= 180^0-35^0-70^0=75^0$
Xét các đáp án trên `-> C (tm)`.
Cho tam giác ABC có: góc A=35 độ. Đường trung trực của AC cắt AB ở D. Biết CD là tia phân giác của góc ACB. số đo các góc góc ABC; góc ACB là:
A. góc ABC= 72 độ; góc ACB= 73 độ
B. góc ABC= 73 độ; góc ACB= 72 độ
C. góc ABC= 75 độ; góc ACB= 70 độ
D. góc ABC= 70 độ; góc ACB=75 độ