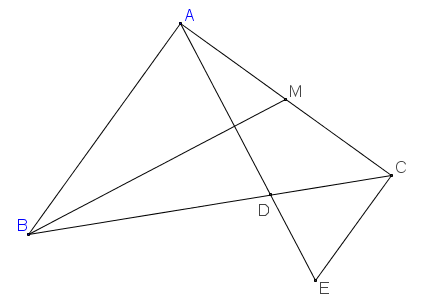
Gọi E là giao điểm của AD và đường thẳng đi qua C , vuông góc với CA
Do AB // CE ( GT ) \(\Rightarrow\dfrac{AB}{CE}=\dfrac{BD}{DC}=2\) ( Định lý Ta - lét )
Vì tam giác ABC cân tại A \(\Rightarrow AB=AC\)
Mà \(AC=2AM\) ( do BM là trung tuyến \(\Rightarrow AM=MC=\dfrac{1}{2}AC\))
\(\Rightarrow AB=2AM\)
\(\Rightarrow\dfrac{2AM}{CE}=2\Rightarrow\dfrac{AM}{CE}=1\Rightarrow AM=CE\)
Xét tam giác BAM và tam giác ACE có :
\(\left\{{}\begin{matrix}AB=AC\left(GT\right)\\\widehat{BAM}=\widehat{ACE}\left(=90^o\right)\\AM=CE\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\) tam giác BAM = tam giác ACE ( c . g . c )
\(\Rightarrow\) góc AMB = góc AEC ( 2 góc t/ứng )
Mà góc AEC + góc CAE = 90 độ
=> góc AMB + góc CAE = 90 độ
=> BM vuông góc với AD ( đpcm )
Kẻ đường thẳng qua C vuông góc AC cắt AD tại E
Ta có $\frac{AB}{CE} =\frac{BD}{CD} =2$ (1)
Mà AB =AC = 2 .AM (2)
Từ (1) và (2) =>$\frac{AM}{CE} =1$ =>AM =CE
=>$\triangle BAM =\triangle ACE$ (c, g, c)
=>$\widehat{ABM} =\widehat{CAE}$
Mà $\widehat{ABM} +\widehat{AMB} =90^\circ$
=>$\widehat{CAE} +\widehat{AMB} =90^\circ$
=>BM vuông góc AD(đpcm)


