Bài 3: Quan hệ giữa ba cạnh của một tam giác bất đẳng thức tam giác
Các câu hỏi tương tự
Bài 5: Cho hình vẽ.
|
a) Chứng minh: EA + EB < DA + DB b)So sánh EA + EB với CA + CB c) Chứng minh: nửa chu vi ∆ ABC < EA + EB + EC < chu vi ∆ ABC
|
|
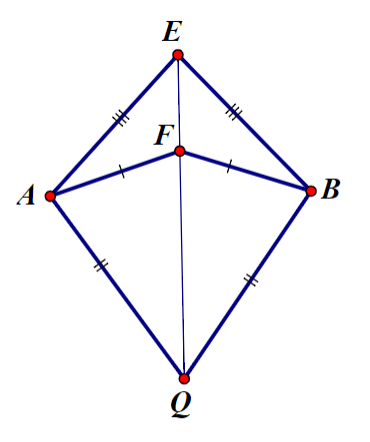
Chohình vẽbên,biết EA EB; FA FB; QA QB.a) Vẽ lại hình và viết giả thiết, kết luậnb) Chứng minh ∆AEF ∆BEF c) Chứng minh ∆AEQ ∆BEQ
Đọc tiếp
Chohình vẽbên,biết EA = EB; FA = FB; QA = QB.
a) Vẽ lại hình và viết giả thiết, kết luận
b) Chứng minh ∆AEF = ∆BEF
c) Chứng minh ∆AEQ = ∆BEQ
Cho ΔABC đều và D là một điểm thuộc cạnh BC. Trên nửa mặt phẳng bờ BC không chứa điểm A, vẽ tia Bx sao cho \(\widehat{CBx} = \widehat{CAD}\). Tia Bx cắt tia AD tại E. Chứng minh rằng: EA = EB + EC.
Cho tam giác ABC ( AC AB ) , kẻ trung tuyến AD . Từ B kẻ BEvuông góc với AD , từ C kẻ CF vuông góc với AD a/ Chứng minh : BED CFD b/ Chứng minh : CE // BF c/ So sánh EB và EC .
Đọc tiếp
Cho tam giác ABC ( AC > AB ) , kẻ trung tuyến AD . Từ B kẻ BE
vuông góc với AD , từ C kẻ CF vuông góc với AD
a/ Chứng minh : ![]() BED =
BED = ![]() CFD
CFD
b/ Chứng minh : CE // BF
c/ So sánh EB và EC .
Cho tam giác ABC có 3 góc nhọn và AB < AC. Vẽ phân giác AD. Lấy F trên AC sao cho AF=AB. Lấy điểm E trên AD với AE < AB (3 điểm B,E,F không thẳng hàng)
a)Chứng minh EB = EF
b) Chứng minh BE + EC > AC - AB
Cho ABC vuông tại A. Trên cạnh BC lấy điểm D sao cho BD=BA.Qua D vẽ đường thẳng vuông góc với BC, cắt AC tại điểm E và cắt tia BA tại điểm K
a/ Chứng minh : Tam giác ABE= tam giác DBE
b/ Chứng minh : EK=EC
c/ BE cắt CK tại M . Chứng minh EB+EK < MB+MK < CB+CK
Cho △ABC, có AB>AC. Kẻ tia phân giác AD của góc A( D∈BC) trên đoạn AD lấy điểm E tùy ý. Chứng minh: AB-AC > EB-EC
Cho tam giác ABC và M là một điểm nằm trong tam giác. Gọi I là giao điểm của đường thẳng BM và cạn AC
a) So sánh IB với MI + IA, từ đó chứng minh MA + MB < IB +IA
b) So sánh IB với IC + CB, từ đó chứng minh IB + IA < CA + CB
c) Chứng minh bất đẳng thức MA + MB < CA + CB
Cho tam giác ABC, điểm D nằm giữa B và C. Chứng minh rằng AD nhỏ hơn nửa chu vi tam giác ABC ?
Cho tam giác ABC. Trên tia đối của AC lấy D sao cho AD= AC. Trên tia đối của tia AB lấy E sao cho AE= AB. Nối D với E
a) Chứng minh tam giác ABC= tam giác ADE
b) Gọi M là trung điểm của BC, N là trung điểm của DE. Chứng minh AM=AN
