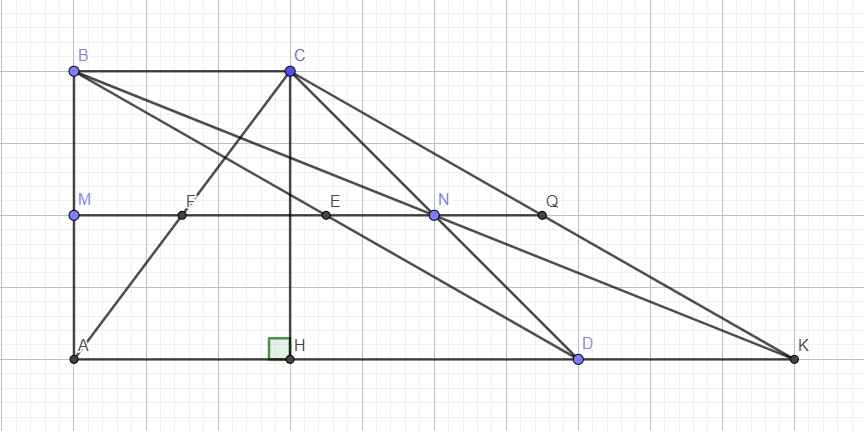
Cho hình thang ABCD vuông tại A và B có D = 45o, BC = 6cm, AB = 8cm.
a) Tính AD, CD.
b) Gọi M, N, E, F là trung điểm của AB, CD, BD, AC. Chứng minh M, N, E, F thẳng hàng.
c) BN cắt AD tại K, EN cắt CK tại Q. Chứng minh BCKD là hình bình hành, QB = QA.
d) Chứng minh: CK^2 = AC^2 + AK^2 - 2.AC.AK.cosKAC
Em làm được a,b rồi ạ. Mong anh chị giúp em câu c,d ạ.
c.
K thuộc AD nên BC song song DK
Áp dụng định lý Talet: \(\dfrac{BN}{KN}=\dfrac{CN}{DN}=1\Rightarrow BN=KN\) hay N là trung điểm BK
\(\Rightarrow\) BCKD là hình bình hành (tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường)
Theo câu b, E, M, N thẳng hàng nên Q nằm trên MN (1)
Mà MN là đường trung bình của hình thang ABCD
\(\Rightarrow MN||AD\Rightarrow MN\perp AB\) (2)
Mà M là trung điểm AB (3)
(2);(3) \(\Rightarrow\) MN là trung trực AB (4)
(1);(4) \(\Rightarrow QB=QA\)
d.
Hạ CH vuông góc AD
Trong tam giác vuông CHK: \(cosKAC=\dfrac{AH}{AC}\Rightarrow AH=AC.cos\widehat{KAC}\)
Pitago: \(CH^2+AH^2=AC^2\)
Do đó: \(CK^2=CH^2+HK^2=CH^2+\left(AK-AH\right)^2=CH^2+AH^2+AK^2-2AK.AH\)
\(=AC^2+AK^2-2AK.AC.cos\widehat{KAC}\) (đpcm)