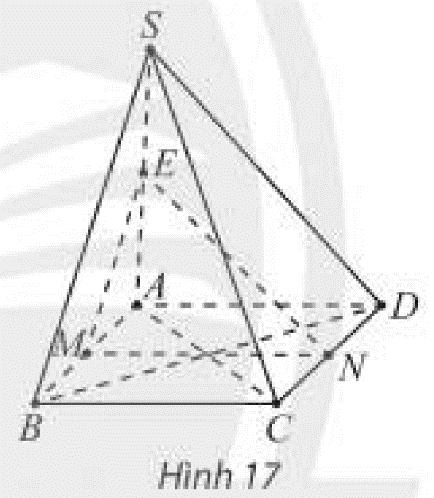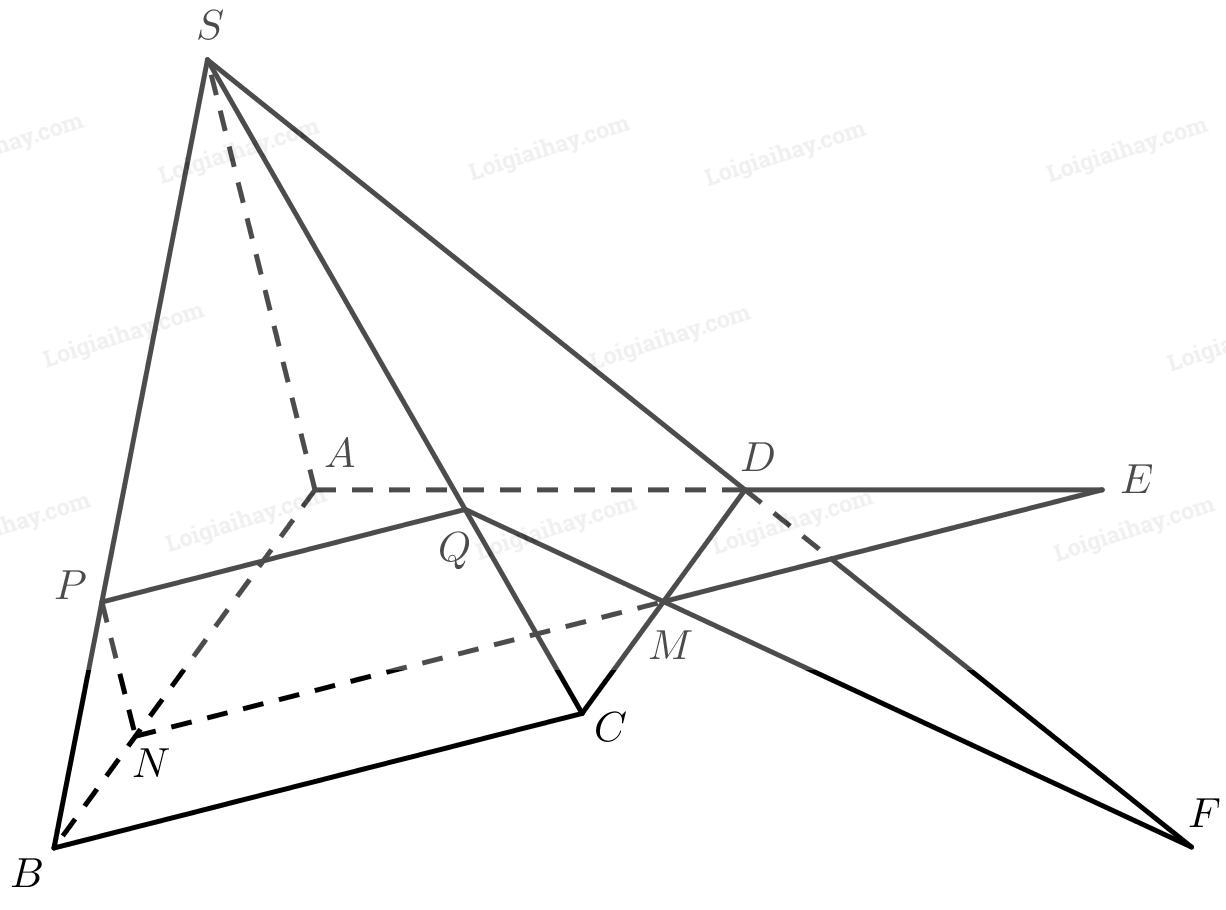
Qua \(M\) dựng đường thẳng song song với \(BC\), cắt \(AB\) tại \(N\).
Qua \(N\) dựng đường thẳng song song với \(SA\), cắt \(SB\) tại \(P\).
Qua \(P\) dựng đường thẳng song song với \(BC\), cắt \(SC\) tại \(Q\).
Vì \(MN\parallel BC,NP\parallel SA\) nên \(\left( {MNPQ} \right) \equiv \left( P \right)\).
Ta có:
\(\begin{array}{l}MN = \left( P \right) \cap \left( {ABC{\rm{D}}} \right)\\NP = \left( P \right) \cap \left( {SAB} \right)\\PQ = \left( P \right) \cap \left( {SBC} \right)\\MQ = \left( P \right) \cap \left( {SC{\rm{D}}} \right)\end{array}\)
Gọi \(E\) là giao điểm của \(A{\rm{D}}\) và \(MN\), \(F\) là giao điểm của \(S{\rm{D}}\) và \(MQ\). Ta có:
\(\begin{array}{l}\left. \begin{array}{l}E \in A{\rm{D}} \subset \left( {SA{\rm{D}}} \right)\\E \in MN \subset \left( P \right)\end{array} \right\} \Rightarrow E \in \left( P \right) \cap \left( {SA{\rm{D}}} \right)\\\left. \begin{array}{l}F \in S{\rm{D}} \subset \left( {SA{\rm{D}}} \right)\\F \in MQ \subset \left( P \right)\end{array} \right\} \Rightarrow F \in \left( P \right) \cap \left( {SA{\rm{D}}} \right)\\ \Rightarrow EF = \left( P \right) \cap \left( {SA{\rm{D}}} \right)\end{array}\)