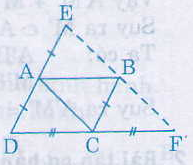
AE // BC (vì AD // BC)
AE = BC (cùng bằng AD)
nên ACBE là hình bình hành.
Suy ra: BE // AC, BE = AC (1)
Tương tự BF // AC, BF = AC (2)
Từ (1) và (2) suy ra E, B, F thẳng hàng và BE = BF. Nên B là trung điểm của EF, vậy E đối xứng với F qua B
Cho Hình bình hành ABCD. Gọi điểm E là điểm đối xứng với D qua điểm A, gọi F là điểm đối xứng với D qua điểm C. CMR điểm E đối xứng với F qua điểm B.
Cho tam giác ABC, D là một điểm trên cạnh BC. Gọi E và F theo thứ tự là điểm đối xứng của điểm D qua AB và AC
a) Chứng minh AE=AF
b) Tam giác ABC phải có thêm điều kiện gì để điểm E đối xứng với điểm F qua điểm A?
Cho tam giác ABC, gọi D, E lần lượt là trung điểm của AB, AC.Gọi o là điểm bất kì nằm trong tam giác ABC. Vẽ M đối xứng với O qua D, vẽ N đối xứng với O qua E. Chứng minh MNCB là hình bình hành
Cho ∆ABC cân tại A và D là điểm đối xứng của A qua BC
a) Gọi F là giao điểm của AD và BC. Tứ giác ABCD là hình gì ? Vì sao ?
b) Gọi E là điểm đối xứng với C qua A. CM : EB vuông BC
c) Tứ giác ADBE là hình gì ? Vì sao ?
d) Đường thẳng AF cắt AB tại G. Chứng minh : GA = 1/2 GB
e) Đường thẳng CG cắt AF tại I. Chứng minh : IA = IF
Cho ▲ABC vuông tại A, đường cao AH. Từ H kẻ \(HE\perp AB\left(E\in AB\right),HF\perp AC\left(F\in AC\right)\)
a) Tứ giác AEHF là hình gì? Vì sao?
b) Gọi M là điểm đối xứng với H qua F. Chứng minh tứ giác AEFM là hình bình hành.
c) Gọi N là điểm đối xứng với H qua E. Chứng minh \(BC^2=BN^2+CM^2+2HB.HC\)
Cho ∆ABC cân tại A và D là điểm đối xứng của A qua BC
a) Gọi F là giao điểm của AD và BC. Tam giác ABCD là hình gì ? Vì sao ?
b) Gọi E là điểm đối xứng với C qua A. Chứng minh : EB vuông BC
c) Tứ giác ADBE là hình gì ? Vì sao ?
d) Đường thẳng AF cắt AB tại G. Chứng minh : GA = 1/2 GB
e) Đường thẳng CG cắt AF tại I. Chứng minh : IA = IF
Cho hình bình hành ABCD có AB = 2AD. Gọi M,N lần lượt là trung điểm của AB,CD
a) chứng minh tứ giác ABCD là hình bình hành
b)chừng minh tứ giác AMND là hình thoi
c)Gọi K là điểm đối xứng vời điểm A qua D.Gọi Q là điểm đối xứng với N qua D.Tứ giác ANKQ là hình gì? Vì sao?
d)Hình bình hành ABCD có thêm điều kiện gì để tứ giác ABCN là hình thang cân
(nhớ vẽ hình nha)
Cho tam giác ABC cân tại AH là đường cao .Gọi M,N lần lượt là rung điểm AB,AC.Biết AH=16cm,BC=12cm
a) Tính diện tích tam giác ABC và độ dài MN
b) Gọi E đối xứng với H qua M.chứng minh tứ giác AHBE là hình chữ nhật
c) gọi F đối xứng F đối xứng A qua H.Chứng minh ABFC là hình thoi
d) Gọi K là hình chiếu của A trên FC.Goi I là trung điểm của HK.chứng minh BK vuông góc với IF
Cho tam giác ABC cân tại AH là đường cao .Gọi M,N lần lượt là rung điểm AB,AC.Biết AH=16cm,BC=12cm
a) Tính diện tích tam giác ABC và độ dài MN
b) Gọi E đối xứng với H qua M.chứng minh tứ giác AHBE là hình chữ nhật
c) gọi F đối xứng F đối xứng A qua H.Chứng minh ABFC là hình thoi
d) Gọi K là hình chiếu của A trên FC.Goi I là trung điểm của HK.chứng minh BK vuông góc với IF