b)
Có: \(cot\alpha=\dfrac{cos\alpha}{sin\alpha}\)
Vì $\alpha $ là góc nhọn nên `0<sin\alpha<1`
\(\Rightarrow\dfrac{cos\alpha}{sin\alpha}>\dfrac{cos\alpha}{1}=cos\alpha\)
Vậy \(cos\alpha< cot\alpha\)
b)
Có: \(cot\alpha=\dfrac{cos\alpha}{sin\alpha}\)
Vì $\alpha $ là góc nhọn nên `0<sin\alpha<1`
\(\Rightarrow\dfrac{cos\alpha}{sin\alpha}>\dfrac{cos\alpha}{1}=cos\alpha\)
Vậy \(cos\alpha< cot\alpha\)
Tìm góc nhọn α , biết sinα = cosα .
Bài 1: Biết rằng sinα = 0,6. Tính cosα và tgα.
Bài 2: Biết rằng cosα = 0,7. Tính sinα và tgα.
Bài 3: Biết rằng tgα = 0,8. Tính sinα và cosα.
Bài 4: Biết cosx = \(\dfrac{1}{2}\), tính P = 3sin2x + 4cos2x.
tính góc α biết sinα= 4/5
Bài 5: Cho góc nhọn α, biết sin α = 2/3. Không tính số đo góc, hãy tính cos α, tan α, cot α
Cho góc nhọn α, biết cos α = \(\dfrac{1}{5}\). Tính sin α, tan α, cot α.
Biết tanα = 0,1512. Số đo góc nhọn α làm tròn đến phút là?
cho △abc vuông tại a, góc b=60 độ, ab<ac. bd là đường phân giác, de ⊥ bc. CMR:
a)△abd=△ebd b)△abe là △ đều c)so sánh ad và dc
4, cho tg ABC cân tại A, đường cao ứng vs cạnh bên có độ dài bằng h, góc ở đáy của tg bằng α. CMR:SABC= 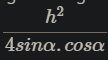
4, cho tg ABC cân tại A, đường cao ứng vs cạnh bên có độ dài bằng h, góc ở đáy của tg bằng α. CMR: \(S^{_{ABC}}=\dfrac{h^2}{4sin\alpha.cos\alpha}\)