\(a\perp\left(P\right)\) tại O
\(OH\subset\left(P\right)\)
Do đó: \(a\perp OH\)
mà \(b\perp OH\)
nên \(d\left(a;b\right)=OH\)
\(a\perp\left(P\right)\) tại O
\(OH\subset\left(P\right)\)
Do đó: \(a\perp OH\)
mà \(b\perp OH\)
nên \(d\left(a;b\right)=OH\)
Nếu đường thẳng a thuộc mặt phẳng (P) và mặt phẳng (Q) song song với (P) thì giữa d(a, (Q)) và d((P),(Q)) có mối quan hệ gì?
a) Cho hai đường thẳng m và n song song với nhau. Khi một điểm M thay đổi trên m thì khoảng cách từ nó đến đường thẳng n có thay đổi hay không?
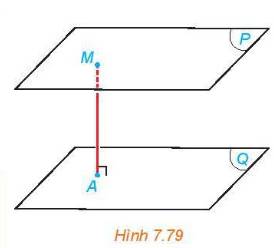
b) Cho hai mặt phẳng song song (P) và (Q) và một điểm M thay đổi trên (P) (H.7.79). Hỏi khoảng cách từ M đến (Q) thay đổi thế nào khi M thay đổi.
Khoảng cách giữa hai hình được nêu trong bài học (điểm, đường thẳng, mặt phẳng) là khoảng cách nhỏ nhất giữa một điểm thuộc hình này và một điểm thuộc hình kia. Hãy thảo luận để làm rõ nhận xét này.
Cho hai đường thẳng chéo nhau a và b. Gọi (Q) là mặt phẳng chứa đường thẳng b và song song với a. Hình chiếu a' của a trên (Q) cắt b tại N. Gọi M là hình chiếu của N trên a (H.7.83).
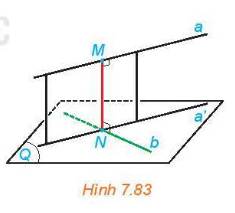
a) Mặt phẳng chứa a và a' có vuông góc với (Q) hay không?
b) Đường thẳng MN có vuông góc với cả hai đường thẳng a và b hay không?
c) Nêu mối quan hệ của khoảng cách giữa a, (Q) và độ dài đoạn thẳng MN.
Cho đường thẳng a song song với mặt phẳng (P). Lấy hai điểm M, N bất kì thuộc a và gọi A, B tương ứng là các hình chiếu của chúng trên (P) (H.7.78).
Giải thích vì sao ABNM là một hình chữ nhật và M, N có cùng khoảng cách đến (P).
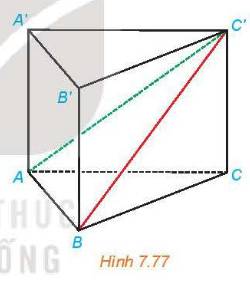
Cho hình lăng trụ đứng ABC.A'B'C' có ABC là tam giác vuông cân tại A, AB = a, AA' = h (H.7.77).
a) Tính khoảng cách từ A đến mặt phẳng (BCC'B').
b) Tam giác ABC' là tam giác gì? Tính khoảng cách từ A đến BC'.
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = a, AB = b, BC = c.
a) Tính khoảng cách giữa CC' và (BB'D'D).
b) Xác định đường vuông góc chung và tính khoảng cách giữa AC và B'D'.
Cho hình chóp S.ABCD có đáy là một hình vuông cạnh a, mặt bên SAD là một tam giác đều và (SAD) ⊥ (ABCD).
a) Tính chiều cao của hình chóp.
b) Tính khoảng cách giữa BC và (SAD).
c) Xác định đường vuông góc chung và tính khoảng cách giữa AB và SD.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, \(SA \bot \left( {ABCD} \right),SA = a\sqrt 2 .\)
a) Tính khoảng cách từ A đến SC.
b) Chứng minh \(BD \bot \left( {SAC} \right).\)
c) Xác định đường vuông góc chung và tính khoảng cách giữa BD và SC.