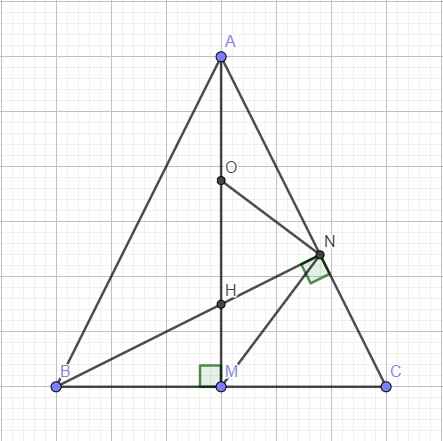
Gọi O là trung điểm AH, tam giác AHN vuông tại N nên N thuộc đường tròn đường kính AH
Do ABC cân tại A \(\Rightarrow\) AM là đường cao đồng thời là trung tuyến
\(\Rightarrow\) M là trung điểm BC
Trong tam giác vuông NBC, NM là trung tuyến ứng với cạnh huyền
\(\Rightarrow MN=MB=\dfrac{1}{2}BC\Rightarrow\Delta MNB\) cân tại M
\(\Rightarrow\widehat{MNB}=\widehat{MBN}\) (1)
Tương tự, trong tam giác vuông ANH, ta có: \(ON=OH=\dfrac{1}{2}AH\Rightarrow\widehat{ONH}=\widehat{OHN}\)
Mà \(\widehat{OHN}=\widehat{MHB}\) (đối đỉnh) \(\Rightarrow\widehat{ONH}=\widehat{MHB}\) (2)
Lại có tam giác HBM vuông tại M \(\Rightarrow\widehat{MHB}+\widehat{MBN}=90^0\) (3)
(1);(2);(3) \(\Rightarrow\widehat{ONH}+\widehat{MNB}=90^0\) hay \(MN\perp ON\)
\(\Rightarrow MN\) là tiếp tuyến của đường tròn đường kính AH