Question

Cho ABC vuông tại B có 60o A  , phân giác góc BAC cắt BC ở D. Kẻ DH vuông góc với AC ( H thuộc AC) a. Chứng minh    ABD AHD b. Chứng minh HA HC  c. So sánh DC và AB d. Gọi I là giao điểm của HD và AB, lấy E là trung điểm của CI. Chứng minh A,D,E thẳng hàng

Answer 1

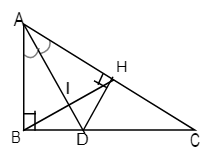
a) Xét ΔABD và ΔAHD có: 

∠ABD = ∠AHD = 90 (gt)

Cạnh AD chung

∠BAD = ∠HAD (gt)

⇒ ΔABD = ΔAHD (ch - gn)

b)  Xét ΔABC có: 

∠B = 90^o 

⇒ ∠A + ∠C =90^o

⇒ ∠C = 90^o − ∠A = 90^o − 60^o = 30^o

Vì AD là tia phân giác của ∠A (gt)

⇒ ∠BAD = ∠DAC = ∠A/2 = 60^o/2 = 30^o

⇒ ∠C = ∠DAC = 30^o 

⇒ ΔADC cân tại D

⇒ AD = DC

⇒ AH = HC (quan hệ giữa đường xiên và hình chiếu)

c) Xét ΔABD có :

AB < AD (cạnh góc vuông < cạnh huyền)

Mà AD = DC (cmt) 

⇒ DC > AB

Answer 2

Hai ý còn lại bạn tự làm nhé mik mỏi tay lắm rùi