Chương I - Hệ thức lượng trong tam giác vuông
Các câu hỏi tương tự
Bài 3: Cho ∆ ABC vuông tại A, đường cao AH biết HB=4cm ; HC= 9cm . a) Tính AB và AH. b) Từ HE vuông góc với AB, HF vuông góc với AC Tử giác AEHF là hình gì? Tính EF ?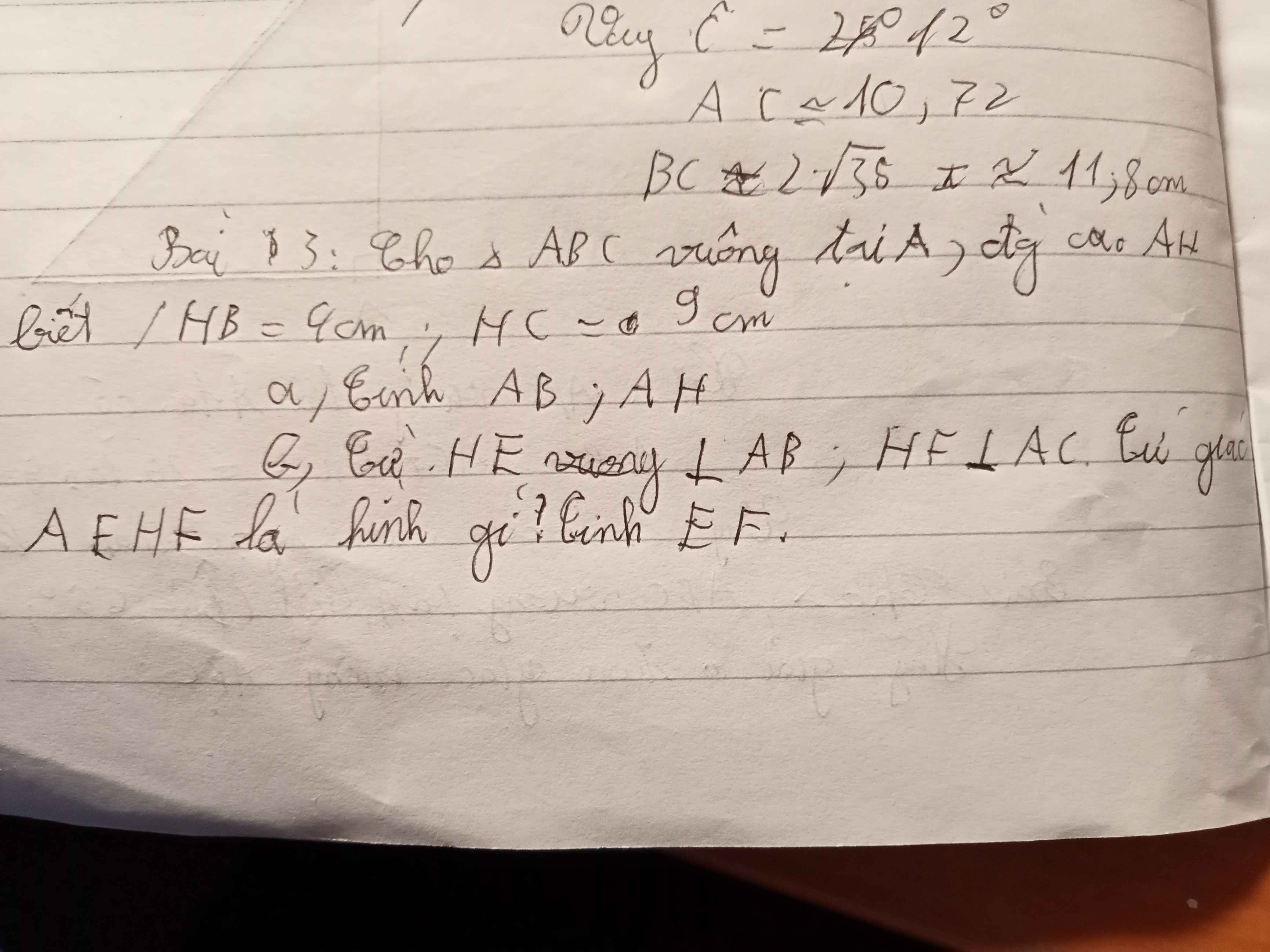
Cho tam giác ABC vuông tại A có đường cao AH.
1) Cho biết AB=3 cm, AC=4 cm. Tính độ dài các đoạn BC,HB,HC,AH
2) Vẽ HE vuông góc với AB tại E, HF vuông góc với AC tại F
a) Chứng minh: AE.EB=HE2
b) Chứng minh: AE.EB+AF.FC=AH2
3) Chứng minh: BE=BC. cos3 B
Cho tam giác ABC vuông tại A, đường cao AH (HϵBC)a) Biết AB 12cm, BC 20cm. Tính AC, B, AH (góc làm tròn đến độ)b) Kẻ HE vuông góc AB (EϵAB). Chứng minh: AE.ABAC2-HC2c) Kẻ HF vuông góc AC (FϵAC). Chứng minh: AFAE.tanC
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH (HϵBC)
a) Biết AB = 12cm, BC = 20cm. Tính AC, B, AH (góc làm tròn đến độ)
b) Kẻ HE vuông góc AB (EϵAB). Chứng minh: AE.AB=AC2-HC2
c) Kẻ HF vuông góc AC (FϵAC). Chứng minh: AF=AE.tanC
cho tam giác abc vuông tại a đường cao ah kẻ hd vuông góc ab he vuông góc ac a, chứng minh adhe là hình chữ nhật b, chứng minh da.db+ea.ec=hb.hc
Cho tam giác ABC vuông tại A, có đường cao AH. Vẽ HE vuông góc AB tại E ; vẽ HF vuông góc AC tại F. Chứng minh: (AE.AB)/(EF.BC) = AF/AB
Cho tam ABC có góc A bằng 90 độ và đường cao AH ( H thuộc BC) kẻ HE và HF lần lượt vuông góc với AB và AC tại E,F
1, chứng minh AEHF là hcn và tính EF , CF
2, tính diện tích tứ giác AEHF
3, tính diện tích tứ giác BEFC
6. Cho tam giác ABC vuông ở A đường cao AH, biết AB = 6cm, AC =8cm. a/ Tính AH; b/ Tính góc HAC; c/ Từ H kẻ HE AB, HF AC. Tính EF
Cho tam giác ABC vuông tại A, có đường cao AH. Vẽ HE vuông góc AB tại E ; vẽ HF vuông góc AC tại F.
Chứng minh: AE.AB=AF.AC
Chứng minh: HB/HC = (AB/AC)2
Cho tam giác ABC vuông tại A,đường cao AH(H thuộc BC) 1/Giả sử AB=6cm,AC=8cm.Tính độ dài BC,AH 2/Kẻ HE vuông góc với AB tại E.Gọi I là trung điểm của HC.Kẻ HF vuông góc với AI tại F. Chứng minh tam giác AEF đồng dạng với tam giác AIB.
Cho tam giác ABC vuông tại C, đường cao CH. Biết AH = 4cm. HB = 9cm
a) Tính CH, CA ?
b) Kẻ HE vuông góc với AC, F vuông góc với BC (E thuộc AC, F thuộc BC) Chứng minh: CE . CA = CF . CB. Từ đó chứng minh: tam giác CEF đồng dạng với tam giác CBA
c) Chứng minh: AB = ACcosA + BCcosB
