Gọi 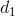 ,
, 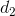 ,
,  là ba đường thẳng đã cho. Gọi I =
là ba đường thẳng đã cho. Gọi I = 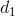 ∩
∩ 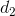
Ta chứng minh I ∈ 
I ∈ 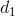 => I ∈ (β) = (
=> I ∈ (β) = ( 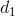 ,
,  )
)
I ∈ 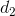 => I ∈ (ɣ) = (
=> I ∈ (ɣ) = ( 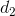 ,
,  )
)
Từ đó suy ra, I ∈ 
Gọi 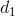 ,
, 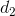 ,
,  là ba đường thẳng đã cho. Gọi I =
là ba đường thẳng đã cho. Gọi I = 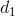 ∩
∩ 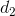
Ta chứng minh I ∈ 
I ∈ 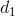 => I ∈ (β) = (
=> I ∈ (β) = ( 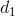 ,
,  )
)
I ∈ 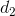 => I ∈ (ɣ) = (
=> I ∈ (ɣ) = ( 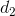 ,
,  )
)
Từ đó suy ra, I ∈ 
cho 3 đường thẳng a, b ,c không cùng nằm trên một mặt phẳng sao cho chúng đôi một cắt nhau . chứng minh rằng chúng đồng quy .
cho 3 đường thẳng a, b ,c không cùng nằm trên một mặt phẳng sao cho chúng đôi một cắt nhau . chứng minh rằng chúng đồng quy .
cho 3 đường thẳng a, b ,c không cùng nằm trên một mặt phẳng sao cho chúng đôi một cắt nhau . chứng minh rằng chúng đồng quy .
cho 3 đường thẳng a, b ,c không cùng nằm trên một mặt phẳng sao cho chúng đôi một cắt nhau . chứng minh rằng chúng đồng quy .
cho 3 đường thẳng a, b ,c không cùng nằm trên một mặt phẳng sao cho chúng đôi một cắt nhau . chứng minh rằng chúng đồng quy .
cho 3 đường thẳng a , b , c không cùng nằm trong một mặt phẳng sao cho chúng đôi một cắt nhau . chứng minh rằng chúng đồng quy
cho 3 đường thẳng a , b , c không cùng nằm trên 1 mặt phẳng sao cho chúng đôi một cắt nhau . chứng minh rằng chúng đồng quy .
cho 3 đường thẳng a , b , c không cùng nằm trên 1 mặt phẳng sao cho chúng đôi một cắt nhau . chứng minh rằng chúng đồng quy .
cho 2 đường thẳng a và b cắt nhau tại O và đường thẳng c cắt mặt phẳng (a,b) tại I khác O . Gọi M là điểm di động trên c và khác I . chứng minh rằng giao tuyến của các mặt phẳng (M,a) và (M,b) cùng nằm trên một mặt phẳng cố định .