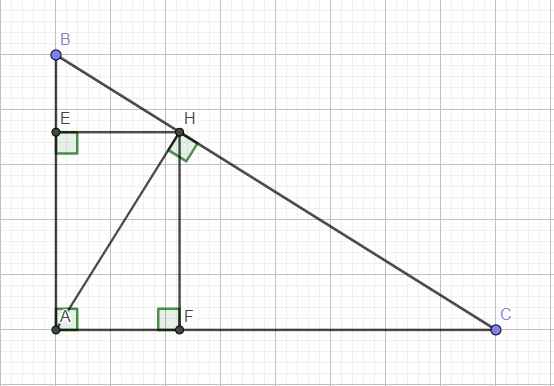
c.
Ta có:
\(sinB=\dfrac{AC}{BC}\)
\(cosC=\dfrac{AC}{BC}\)
\(\Rightarrow cosC=sinB\)
Lại có: \(cosB=\dfrac{AB}{BC}\)
\(\Rightarrow sin^2B+cos^2B=\dfrac{AC^2}{BC^2}+\dfrac{AB^2}{BC^2}=\dfrac{AC^2+AB^2}{BC^2}=\dfrac{BC^2}{BC^2}=1\)
Do đó:
\(\dfrac{sinB+5cosC}{sin^4B+cos^4B+2sin^2B.cos^2B}=\dfrac{sinB+5sinB}{\left(sin^2B+cos^2B\right)^2}=\dfrac{6sinB}{1^2}=6sinB\) (đpcm)