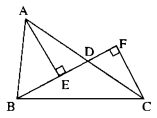
Xét ∆ADE vuông tại E có AD là cạnh huyền:
\(\Rightarrow\) AE < AD (1)
Xét ∆CFD vuông tại F có DC là cạnh huyền
\(\Rightarrow\) FC < DC (2)
Từ (1) và (2), suy ra:
AE + FC < AD + DC
hay AE + FC < AC
Cho tam giác ABC, điểm D nằm giữa A và C (BD không vuông góc với AC). Gọi E và F là chân các đường vuông góc kẻ tử A và C đến đường thẳng BD. So sánh AC với tổng AE + CF ?
Cho tam giác ABC vuông cân tại A , điểm D nằm giữa B và C ( AD không vuông góc với BC ) . Gọi E và F là hình chiếu của B và C trên AD a) So sánh BC với BE + CF b) Tam giác ABE = tam giác CAF c)BE mũ 2 + CF mũ 2 = AB mũ 2 d) gọi m là trung điểm của BC , chứng minh tam giác MBE = tam giác MAF e ) Tam giác MEF vuông cân
Cho mik hỏi:
Câu 1:
Cho tam giác nhọn ABC. Vẽ tia Ax nằm trong góc BAC, Ax cắt BC ở M. Gọi E và F theo thứ tự là hình chiếu của B và C trên tia Ax. Hãy so sánh BE+CF với BC A.BE + CF < BC B.BE + CF > BC C.BE + CF = BC Câu 2: Cho ΔABC vuông tại A, M là trung điểm của AC. Gọi D, E lần lượt là hình chiếu của A và C xuống đường thẳng BM. So sánh BD + BE và AB A.BD+ BE < 2AB B.BD +BE>2AB C.BD + BE = 2AB D.BD + BE < AB Câu 3: Cho tam giác ABC có BD, CE là hai đường cao. So sánh BD + CE và AB + AC A.BD+ CE <AB+ AC B.BD+ CE >AB+ AC C.BD+ CE =AB+ AC Câu 4: Cho tam giác ABC vuông tại A. Trên cạnh AB, AC lần lượt lấy các điểm D, E (D, E không trùng với các đỉnh của tam giác ABC). Chọn đáp án đúng nhất? A.DE > BE < BC B.DE < BE > BC C.DE > BE > BC D.DE < BE < BC Câu 5: Cho tam giác nhọn ABC. Vẽ tia Ax nằm trong góc BAC, Ax cắt BC ở M. Gọi E và F theo thứ tự là hình chiếu của B và C trên tia Ax. Tổng độ dài BE và CF lớn nhất bằng độ dài cạnh nào? A.AB B.AC C.BC D.Không bằng cạnh nào Mik cảm ơn mọi người. Mong mọi người giúp. Nếu đc cho mình xin hình vẽ luôn ạ. Thanks5>Cho tam giác ABC, điểm P nằm giữa A và C Gọi E,F là chân đường vuông góc từ A và C đến BD.CM AC>AE+CE
6>Cho tam giác ABC nhọn, vẽ AD vuông BC, BE vuông AC CM AD+BE
Cho mik hỏi:
Câu 1:
Cho tam giác nhọn ABC. Vẽ tia Ax nằm trong góc BAC, Ax cắt BC ở M. Gọi E và F theo thứ tự là hình chiếu của B và C trên tia Ax. Hãy so sánh BE+CF với BC
A.BE + CF < BC B.BE + CF > BC C.BE + CF = BC
Câu 2: Cho ΔABC vuông tại A, M là trung điểm của AC. Gọi D, E lần lượt là hình chiếu của A và C xuống đường thẳng BM. So sánh BD + BE và AB
A.BD+ BE < 2AB B.BD +BE>2AB C.BD + BE = 2AB D.BD + BE < AB
Câu 3: Cho tam giác ABC có BD, CE là hai đường cao. So sánh BD + CE và AB + AC
A.BD+ CE <AB+ AC B.BD+ CE >AB+ AC C.BD+ CE =AB+ AC
Câu 4: Cho tam giác ABC vuông tại A. Trên cạnh AB, AC lần lượt lấy các điểm D, E (D, E không trùng với các đỉnh của tam giác ABC). Chọn đáp án đúng nhất?
A.DE > BE < BC B.DE < BE > BC C.DE > BE > BC D.DE < BE < BC
Câu 5: Cho tam giác nhọn ABC. Vẽ tia Ax nằm trong góc BAC, Ax cắt BC ở M. Gọi E và F theo thứ tự là hình chiếu của B và C trên tia Ax. Tổng độ dài BE và CF lớn nhất bằng độ dài cạnh nào?
A.AB B.AC C.BC D.Không bằng cạnh nào
Mik cảm ơn mọi người. Mong mọi người giúp. Nếu đc cho mình xin hình vẽ luôn ạ. Thanks
Cho tam giác ABC vuông tại B. Trên cạnh BC lấy các điểm D và E (D nằm giữa B và E).
a) So sánh độ dài các đoạn thẳng AB, AD, AE, AC
b) Vẽ BI, BK, BH lần lượt vuông góc với AD, AE, AC. So sánh các góc ABH, ABK, ABI.
cho tam giác ABC có AB khác AC. M nằm giữa B và C. E và F lần lượt là hình chiếu của B và C xuống AM. So sánh BE+CF với BC
Cho ΔABC. M là một điểm bất kì thuộc đoạn thẳng AC. Gọi E, F là chân đường vuông góc hạ từ A, C tới đường thẳng BM
a) So sánh AE+CF với AC. Xác định vị trí của M để AE+CF có tổng độ dài lớn nhất
b) So sánh AE+CF với nửa chu vi ΔABC
c) Khi ΔABC vuông tại A và M là trung điểm của AC, chứng minh rằng:\(AB< \dfrac{BE+CF}{2}< BC\)
Cho tam giác ABC có AB khác AC. Lấy điểm M sao cho M nằm giữa B và C. Gọi E, F lần lượt là hình chiếu của B và C xuống AM. So sánh BE+CF với BC.