1.

a) Tính gia tốc của ô tô trên 4 đoạn đường trong Hình 8.1.
b) Gia tốc của ô tô trên đoạn đường 4 có gì đặc biệt so với sự thay đổi vận tốc trên các đoạn đường khác?
2. Một con báo đang chạy với vận tốc 30 m/s thì chuyển động chậm dần khi tới gần một con suối. Trong 3 giây, vận tốc của nó giảm còn 9 m/s. Tính gia tốc của con báo.
3. Đồ thị ở Hình 8.2 mô tả sự thay đổi vận tốc theo thời gian trong chuyển động của một ô tô thể thao đang chạy thử về phía Bắc.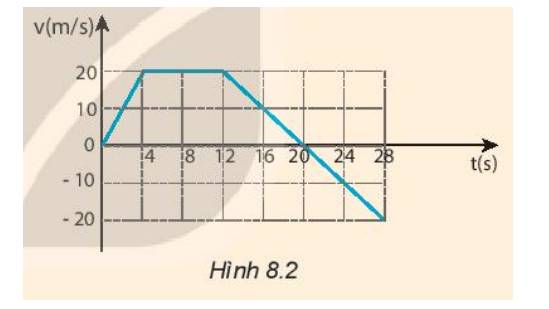
Tính gia tốc của ô tô:
a) Trong 4 s đầu.
b) Từ giây thứ 4 đến giây thứ 12.
c) Từ giây thứ 12 đến giây thứ 20.
d) Từ giây thứ 20 đến giây thứ 28.
1.
a) Đổi 5 km/h = \(\frac{{25}}{{18}}\)m/s; 29 km/h = \(\frac{{145}}{{18}}\)m/s; 49 km/h = \(\frac{{245}}{{18}}\); 30 km/h = \(\frac{{25}}{3}\)m/s
+ Gia tốc trong đoạn đường 1: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{25}}{{18.1}} = \frac{{25}}{{18}} \approx 1,39(m/{s^2})\)
+ Gia tốc trong đoạn đường 2: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{\frac{{145}}{{18}} - \frac{{25}}{{18}}}}{{4 - 1}} \approx 2,22(m/{s^2})\)
+ Gia tốc trong đoạn đường 3: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{\frac{{245}}{{18}} - \frac{{145}}{{18}}}}{{6 - 4}} \approx 2,78(m/{s^2})\)
+ Gia tốc trong đoạn đường 4: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{\frac{{25}}{3} - \frac{{245}}{{18}}}}{{7 - 6}} \approx - 5,28(m/{s^2})\)
b) Trong 4 đoạn đường trên, vận tốc tăng dần, còn gia tốc từ đoạn đường 1 đến đoạn đường 3 tăng dần, nhưng từ đoạn đường 3 đến đoạn đường 4 thì gia tốc giảm dần.
2.
Gia tốc của con báo là:
\(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{9 - 30}}{3} = - 7(m/{s^2})\)
3.
a) Trong 4 s đầu:
\(\begin{array}{l}\Delta v = 20(m/s);\Delta t = 4(s)\\ \Rightarrow a = \frac{{\Delta v}}{{\Delta t}} = \frac{{20}}{4} = 5(m/{s^2})\end{array}\)
b) Từ giây thứ 4 đến giây thứ 12
\(\begin{array}{l}\Delta v = 20 - 20 = 0(m/s);\Delta t = 12 - 4 = 8(s)\\ \Rightarrow a = \frac{{\Delta v}}{{\Delta t}} = 0(m/{s^2})\end{array}\)
c) Từ giây thứ 12 đến giây thứ 20:
\(\begin{array}{l}\Delta v = 0 - 20 = - 20(m/s);\Delta t = 20 - 12 = 8(s)\\ \Rightarrow a = \frac{{\Delta v}}{{\Delta t}} = \frac{{ - 20}}{8} = - 2,5(m/{s^2})\end{array}\)
d) Từ giây thứ 20 đến giây thứ 28:
\(\begin{array}{l}\Delta v = - 20 - 0 = - 20(m/s);\Delta t = 28 - 20 = 8(s)\\ \Rightarrow a = \frac{{\Delta v}}{{\Delta t}} = \frac{{ - 20}}{8} = - 2,5(m/{s^2})\end{array}\)


