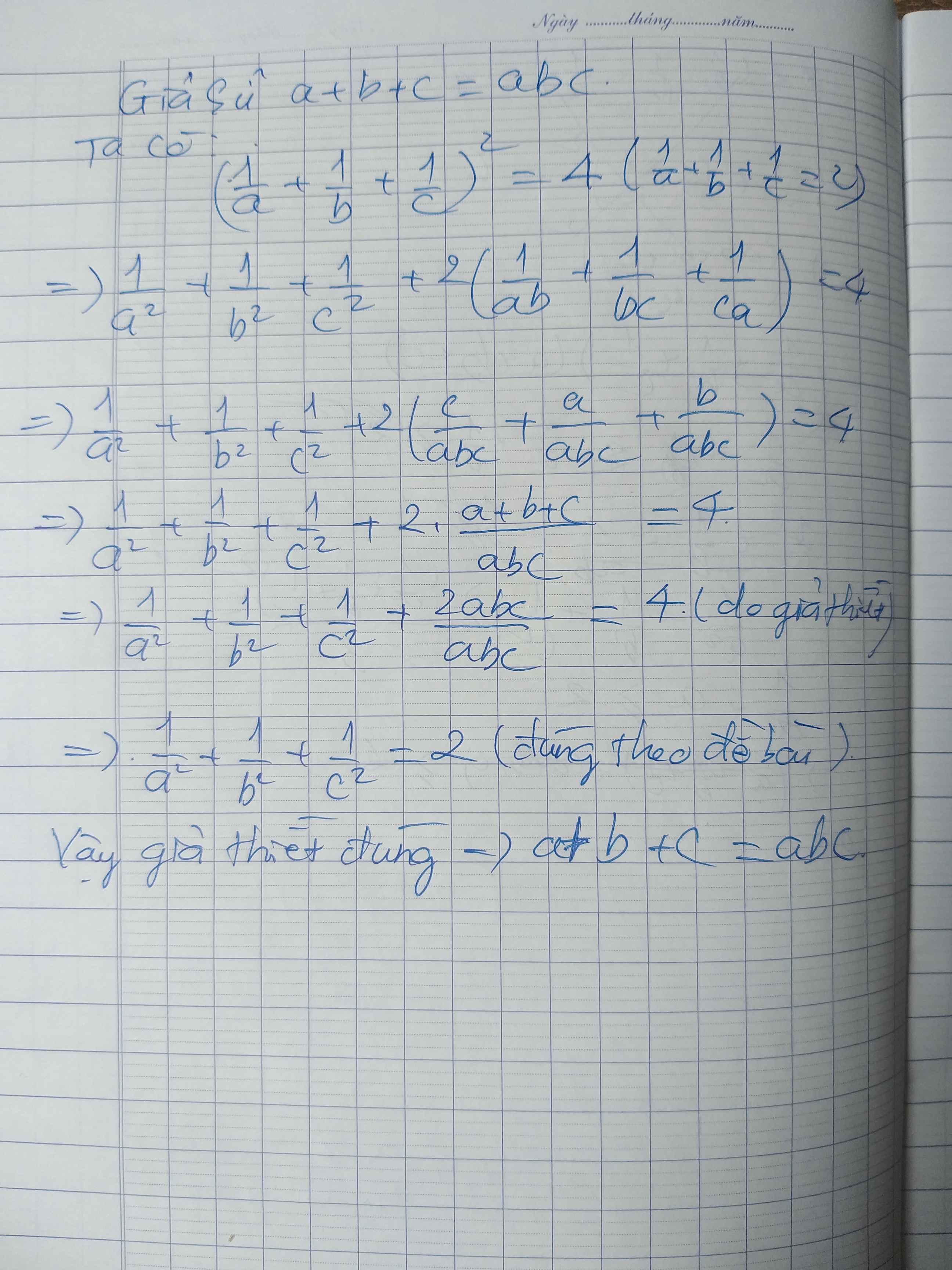113.
\(\dfrac{x^2}{2}+\dfrac{y^2}{3}+\dfrac{z^2}{4}=\dfrac{x^2+y^2+z^2}{5}\)
\(\Leftrightarrow\dfrac{x^2}{2}-\dfrac{x^2}{5}+\dfrac{y^2}{3}-\dfrac{y^2}{5}+\dfrac{z^2}{4}-\dfrac{z^2}{5}=0\)
\(\Leftrightarrow\dfrac{3}{10}x^2+\dfrac{2}{15}y^2+\dfrac{1}{20}z^2=0\)
Do \(x^2;y^2;z^2\ge0;\forall x;y;z\)
\(\Rightarrow\dfrac{3}{10}x^2+\dfrac{2}{15}y^2+\dfrac{1}{20}z^2\ge0;\forall x;y;z\)
Dấu "=" xảy ra khi và chỉ khi \(x=y=z=0\)
114.
\(x^2+y^2+\dfrac{1}{x^2}+\dfrac{1}{y^2}=4\)
\(\Leftrightarrow\left(x^2-2+\dfrac{1}{x^2}\right)+\left(y^2-2+\dfrac{1}{y^2}\right)=0\)
\(\Leftrightarrow\left(x-\dfrac{1}{x}\right)^2+\left(y-\dfrac{1}{y}\right)^2=0\)
Do \(\left\{{}\begin{matrix}\left(x-\dfrac{1}{x}\right)^2\ge0\\\left(y-\dfrac{1}{y}\right)^2\ge0\end{matrix}\right.\) ;\(\forall x;y\ne0\)
\(\Rightarrow\left(x-\dfrac{1}{x}\right)^2+\left(y-\dfrac{1}{y}\right)^2\ge0\)
Dấu "=" xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}x-\dfrac{1}{x}=0\\y-\dfrac{1}{y}=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\pm1\\y=\pm1\end{matrix}\right.\)
115.
Từ giả thiết: \(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=2\)
\(\Rightarrow\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2=4\)
\(\Rightarrow\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}+\dfrac{2}{ab}+\dfrac{2}{bc}+\dfrac{2}{ca}=4\)
\(\Rightarrow2+\dfrac{2}{ab}+\dfrac{2}{bc}+\dfrac{2}{ca}=4\)
\(\Rightarrow\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}=1\)
\(\Rightarrow\dfrac{a+b+c}{abc}=1\)
\(\Rightarrow a+b+c=abc\)
116.
Đặt \(\left\{{}\begin{matrix}\dfrac{a}{x}=m\\\dfrac{b}{y}=n\\\dfrac{c}{z}=p\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m+n+p=2\\\dfrac{1}{m}+\dfrac{1}{n}+\dfrac{1}{p}=0\end{matrix}\right.\)
Từ \(\dfrac{1}{m}+\dfrac{1}{n}+\dfrac{1}{p}=0\)
\(\Rightarrow\dfrac{mn+np+mp}{mnp}=0\)
\(\Rightarrow mn+np+mp=0\) (1)
Lại có:
\(m+n+p=2\)
\(\Rightarrow\left(m+n+p\right)^2=4\)
\(\Rightarrow m^2+n^2+p^2+2\left(mn+np+mp\right)=4\) (2)
(1);(2) \(\Rightarrow m^2+n^2+p^2=4\)
Hay \(\dfrac{a^2}{x^2}+\dfrac{b^2}{y^2}+\dfrac{c^2}{z^2}=4\)
117.
Từ \(\left(a+b+c\right)^2=a^2+b^2+c^2\)
\(\Rightarrow a^2+b^2+c^2+2\left(ab+bc+ca\right)=a^2+b^2+c^2\)
\(\Rightarrow ab+bc+ca=0\)
Chia 2 vế cho abc:
\(\Rightarrow\dfrac{ab+bc+ca}{abc}=0\)
\(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=0\)
\(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}=-\dfrac{1}{c}\)
\(\Rightarrow\left(\dfrac{1}{a}+\dfrac{1}{b}\right)^3=\left(-\dfrac{1}{c}\right)^3\)
\(\Rightarrow\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{3}{ab}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)=-\dfrac{1}{c^3}\)
\(\Rightarrow\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{3}{ab}\left(-\dfrac{1}{c}\right)=-\dfrac{1}{c^3}\)
\(\Rightarrow\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}=\dfrac{3}{abc}\)
118.
Đặt \(\left\{{}\begin{matrix}\dfrac{a}{b}=x\\\dfrac{b}{c}=y\\\dfrac{c}{a}=z\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}xyz=\dfrac{a}{b}.\dfrac{b}{c}.\dfrac{c}{a}=1\left(1\right)\\x+y+z=\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\end{matrix}\right.\)
Từ \(x+y+z=\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\)
\(\Rightarrow x+y+z=\dfrac{xy+yz+zx}{xyz}\)
\(\Rightarrow x+y+z=xy+yz+zx\) (do \(xyz=1\)) (2)
Cộng vế (1) và (2):
\(\Rightarrow xyz+x+y+z=xy+yz+zx+1\)
\(\Rightarrow\left(xyz-xy\right)-\left(yz-y\right)-\left(zx-x\right)+z-1=0\)
\(\Rightarrow xy\left(z-1\right)-y\left(z-1\right)-x\left(z-1\right)+\left(z-1\right)=0\)
\(\Rightarrow\left(z-1\right)\left(xy-y-x+1\right)=0\)
\(\Rightarrow\left(z-1\right)\left[y\left(x-1\right)-\left(x-1\right)\right]=0\)
\(\Rightarrow\left(z-1\right)\left(x-1\right)\left(y-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\y=1\\z=1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\dfrac{a}{b}=1\\\dfrac{b}{c}=1\\\dfrac{c}{a}=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}a=b\\b=c\\c=a\end{matrix}\right.\)
hay trong 3 số luôn tồn tại 2 số bằng nhau
119a.
ĐKXĐ: \(x\ne3\)
\(A=\dfrac{2x^3-6x^2+x-8}{x-3}=\dfrac{2x^2\left(x-3\right)+\left(x-3\right)-5}{x-3}\)
\(=\dfrac{\left(x-3\right)\left(2x^2+1\right)-5}{x-3}=2x^2+1-\dfrac{5}{x-3}\)
Do \(2x^2+1\) nguyên khi x nguyên
\(\Rightarrow A\) nguyên khi \(\dfrac{5}{x-3}\) nguyên
\(\Rightarrow x-3\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\)
\(\Rightarrow x\in\left\{-2;2;4;8\right\}\)
119b.
ĐKXĐ: \(x\ne1\)
\(B=\dfrac{x^4-2x^3-3x^2+8x-1}{x^2-2x+1}\)
\(=\dfrac{\left(x^4-2x^3+x^2\right)-\left(4x^2-8x+4\right)+3}{x^2-2x+1}\)
\(=\dfrac{x^2\left(x-1\right)^2-4\left(x-1\right)^2+3}{\left(x-1\right)^2}\)
\(=\dfrac{\left(x^2-4\right)\left(x-1\right)^2+3}{\left(x-1\right)^2}\)
\(=x^2-4+\dfrac{3}{\left(x-1\right)^2}\)
A nguyên khi \(\dfrac{3}{\left(x-1\right)^2}\) nguyên
\(\Rightarrow\left(x-1\right)^2=Ư\left(3\right)\)
Mà \(\left(x-1\right)^2\) là SCP
\(\Rightarrow\left(x-1\right)^2=1\Rightarrow\left[{}\begin{matrix}x=2\\x=0\end{matrix}\right.\)
119c.
\(C=\dfrac{x^4+3x^3+2x^2+6x-2}{x^2+2}=\dfrac{\left(x^4+2x^2\right)+\left(3x^3+6x\right)-2}{x^2+2}\)
\(=\dfrac{x^2\left(x^2+2\right)+3x\left(x^2+2\right)-2}{x^2+2}\)
\(=\dfrac{\left(x^2+2\right)\left(x^2+3x\right)-2}{x^2+2}\)
\(=x^2+3x-\dfrac{2}{x^2+2}\)
A nguyên khi \(\dfrac{2}{x^2+2}\) nguyên
\(\Rightarrow x^2+2=Ư\left(2\right)\)
Mà \(x^2+2\ge2;\forall x\)
\(\Rightarrow x^2+2=2\)
\(\Rightarrow x=0\)