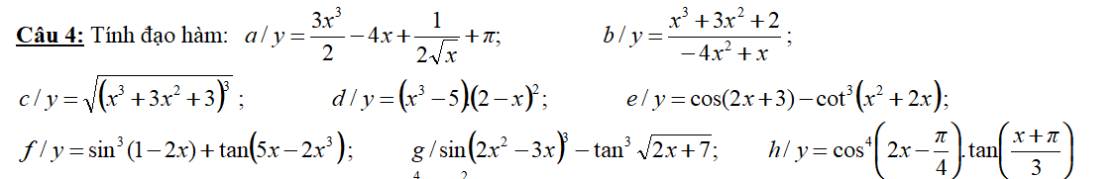a.
\(y'=\dfrac{9x^2}{2}-4-\dfrac{1}{4\sqrt{x^3}}\)
b.
\(y'=\dfrac{\left(3x^2+6x\right)\left(-4x^2+x\right)-\left(x^3+3x^2+2\right)\left(-8x+1\right)}{\left(-4x^2+x\right)^2}=\dfrac{-4x^4+2x^3+3x^2+16x-2}{\left(4x^2-x\right)^2}\)
c.
\(y'=\left[\left(x^3+3x^2+3\right)^3\right]'.\dfrac{1}{2\sqrt{\left(x^3+3x^2+3\right)^3}}=\dfrac{3\left(x^3+3x^2+3\right)^2.\left(x^3+3x^2+3\right)'}{2\sqrt{\left(x^3+3x^2+3\right)^3}}\)
\(=\dfrac{3\left(x^3+3x^2+3\right)^2\left(3x^2+6x\right)}{2\sqrt{\left(x^3+3x^2+3\right)^3}}=\dfrac{9}{2}\left(x^2+2x\right)\sqrt{x^3+3x^2+3}\)
d.
\(y=\left(x^3-5\right)\left(x^2-4x+4\right)\Rightarrow y'=3x^2\left(x^2-4x+4\right)+\left(x^3-5\right)\left(2x-4\right)\)
e.
\(y'=-2sin\left(2x+3\right)-3cot^2\left(x^2+2x\right).\left[cot\left(x^2+2x\right)\right]'\)
\(=-2sin\left(2x+3\right)-3cot^2\left(x^2+2x\right).\dfrac{-\left(2x+2\right)}{sin^2\left(x^2+2x\right)}\)
f.
\(y'=3sin^2\left(1-2x\right).\left[sin\left(1-2x\right)\right]'+\dfrac{5-6x^2}{cos^2\left(5x-2x^3\right)}\)
\(=-6sin^2\left(1-2x\right).cos\left(1-2x\right)+\dfrac{5-6x^2}{cos^2\left(5x-2x^3\right)}\)
g.
\(y'=cos\left(2x^2-3x\right)^3.\left[\left(2x^2-3x\right)^3\right]'-3tan^2\sqrt{2x+7}.\left[tan\sqrt{2x+7}\right]'\)
\(=3\left(2x^2-3x\right)^2\left(4x-3\right).cos\left(2x^2-3x\right)^3-3tan^2\sqrt{2x+7}.\dfrac{1}{\sqrt{2x+7}.cos^2\sqrt{2x+7}}\)
h.
\(y'=4cos^3\left(2x-\dfrac{\pi}{4}\right)\left[cos\left(2x-\dfrac{\pi}{4}\right)\right]'.tan\left(\dfrac{x+\pi}{3}\right)+cos^4\left(2x-\dfrac{\pi}{4}\right).\dfrac{1}{3cos^2\left(\dfrac{x+\pi}{3}\right)}\)
\(=-8cos^3\left(2x-\dfrac{\pi}{4}\right).sin\left(2x-\dfrac{\pi}{4}\right)+cos^4\left(2x-\dfrac{\pi}{4}\right).\dfrac{1}{3cos^2\left(\dfrac{x+\pi}{3}\right)}\)