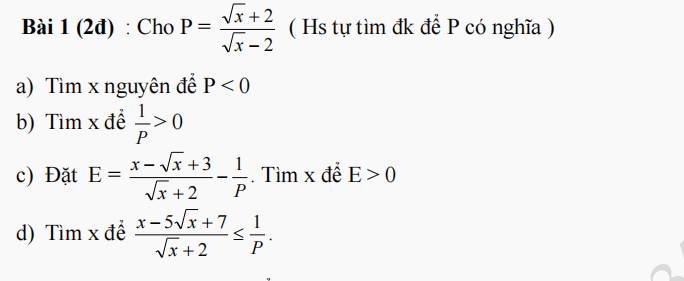a) Để P<0 \(\left(Đk:x\ge0;x\ne4\right)\)
=> \(\left\{{}\begin{matrix}\sqrt{x}+2>0\\\sqrt{x}-2< 0\end{matrix}\right.\)\(\Rightarrow0\le x< 4\)
b) \(\dfrac{1}{P}=\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\) >0 \(\Leftrightarrow\sqrt{x}-2>0\Leftrightarrow x>4\)
c) \(E=\dfrac{x-\sqrt{x}+3-\left(\sqrt{x}-2\right)}{\sqrt{x}+2}=\dfrac{x-2\sqrt{x}+5}{\sqrt{x}+2}=\dfrac{\left(\sqrt{x}-1\right)^2+4}{\sqrt{x}+2}\)
E>0 \(\forall\ge0\)
d) \(\dfrac{x-5\sqrt{x}+7}{\sqrt{x}+2}\le\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)
\(\Leftrightarrow x-5\sqrt{x}+7\le\sqrt{x}-2\)
\(\Leftrightarrow x-6\sqrt{x}+9\le0\)
\(\Leftrightarrow\left(\sqrt{x}-3\right)^2\le0\)
\(\Leftrightarrow x=9\left(\text{vì }\left(\sqrt{x}-3\right)^2\ge0\forall x\ge0\right)\)