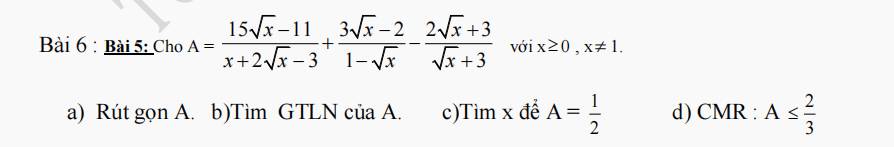a: \(A=\dfrac{15\sqrt{x}-11-\left(3\sqrt{x}-2\right)\left(\sqrt{x}+3\right)-\left(2\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{15\sqrt{x}-11-3x-9\sqrt{x}+2\sqrt{x}+6-2x+2\sqrt{x}-3\sqrt{x}+3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{-5x+7\sqrt{x}-2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}=\dfrac{-\left(5\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}=\dfrac{-5\sqrt{x}+2}{\sqrt{x}+3}\)
b: A=1/2
=>\(\dfrac{-5\sqrt{x}+2}{\sqrt{x}+3}=\dfrac{1}{2}\)
=>-10căn x+4=căn x+3
=>-11căn x=-1
=>căn x=1/11
=>x=1/121
d: \(A-\dfrac{2}{3}=\dfrac{-5\sqrt{x}+2}{\sqrt{x}+3}-\dfrac{2}{3}\)
\(=\dfrac{-10\sqrt{x}+6-2\sqrt{x}-6}{3\left(\sqrt{x}+3\right)}=-\dfrac{12\sqrt{x}}{3\left(\sqrt{x}+3\right)}< =0\)
=>A<=2/3