\(\left(x+1\right)\sqrt{x^2-2x+3}=x^2+1\)
\(\Leftrightarrow\left(x+1\right)^2\left(x^2-2x+3\right)=\left(x^2+1\right)^2\)
\(\Leftrightarrow\left(x^2+2x+1\right)\left(x^2-2x+3\right)=x^4+2x^2+1\)
\(\Leftrightarrow x^4-2x^3+3x^2+2x^3-4x^2+6x+x^2-2x+3=x^4+2x^2+1\)
\(\Leftrightarrow x^4+4x+3=x^4+2x^2+1\)
\(\Leftrightarrow x^4-x^4+4x+3-2x^2-1=0\)
\(\Leftrightarrow-2x^2+4x+2=0\)
\(\Leftrightarrow-2\left(x^2-2x-1\right)=0\)
\(\Leftrightarrow x^2-2x-1=0\)
\(\Rightarrow\Delta=\left(-2\right)^2-4\cdot1\cdot-1=8\)
\(\Leftrightarrow\left[{}\begin{matrix}x_1=\dfrac{2+\sqrt{8}}{2}=1+\sqrt{2}\\x_2=\dfrac{2-\sqrt{8}}{2}=1-\sqrt{2}\end{matrix}\right.\)
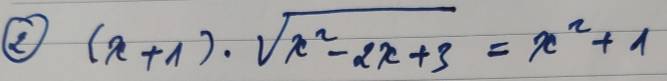





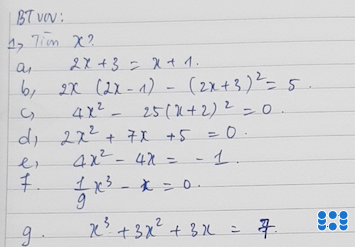
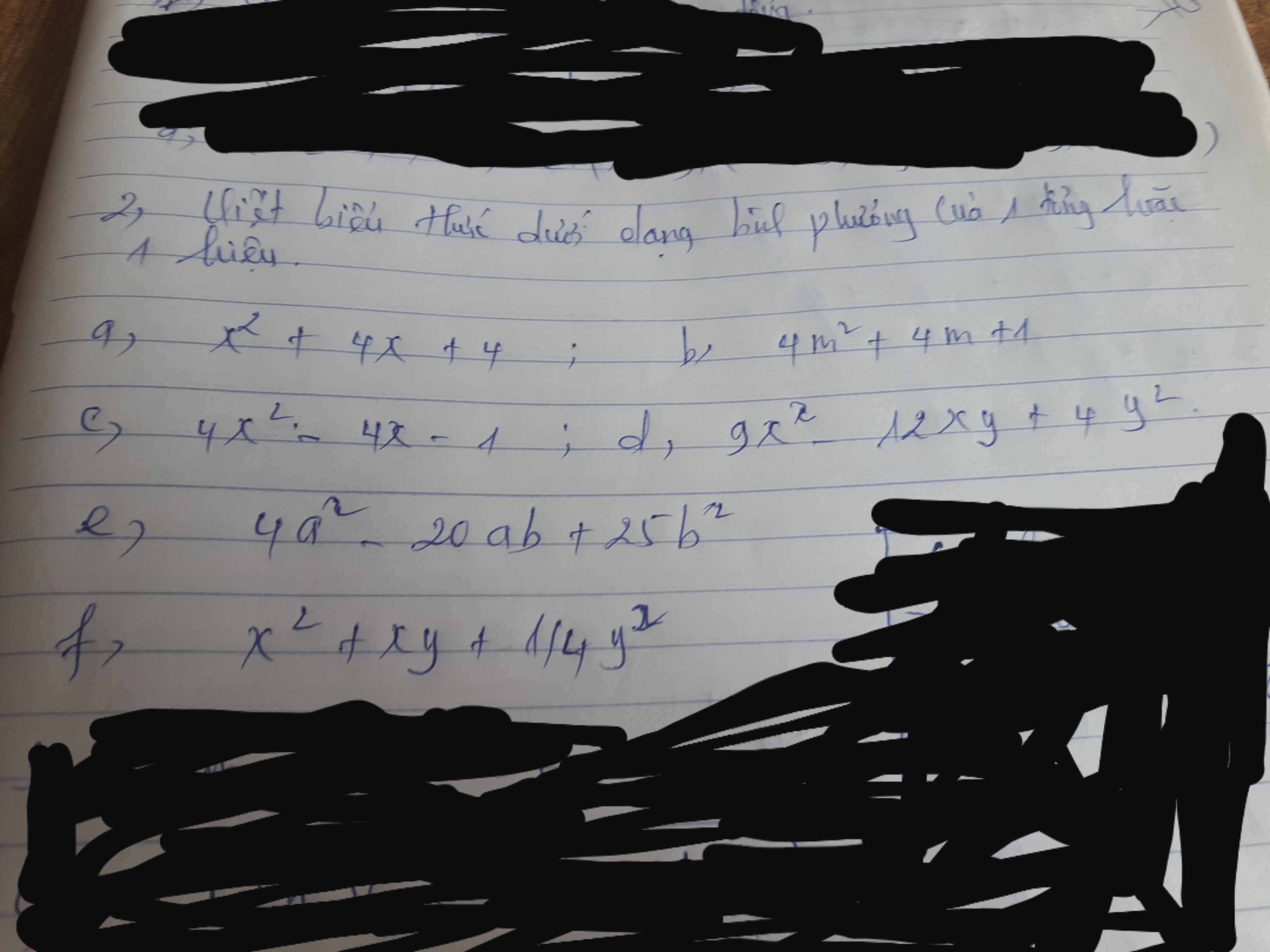

 giải thích giùm mình với
giải thích giùm mình với