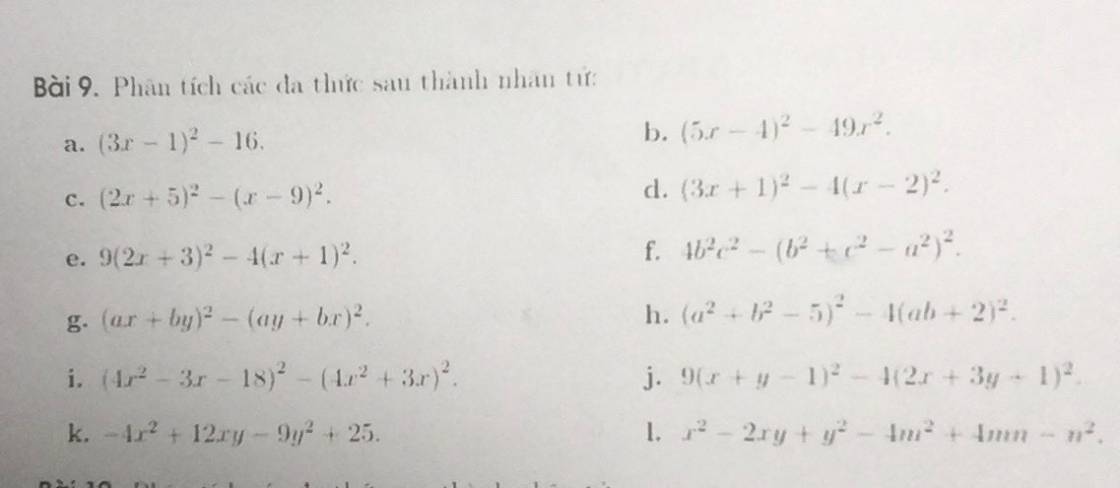\(a,\left(3x-1\right)^2-16=\left(3x-1\right)^2-4^2=\left(3x-1-4\right)\left(3x-1+4\right)\\ =\left(3x-5\right)\left(3x+3\right)=3\left(3x-5\right)\left(x+1\right)\\ b,\left(5x-4\right)^2-49x^2=\left(5x-4\right)^2-\left(7x\right)^2\\ =\left(5x-4+7x\right)\left(5x-4-7x\right)\\ =\left(12x-4\right)\left(-2x-4\right)\\ =-4\left(x-3\right).2.\left(x+2\right) =-8.\left(x-3\right)\left(x+2\right)\\ c,\left(2x+5\right)^2-\left(x-9\right)^2=\left[\left(2x+5\right)-\left(x-9\right)\right]\left[\left(2x+5\right)+\left(x-9\right)\right]\\ =\left(x-4\right)\left(3x-4\right)\\ d,\left(3x+1\right)^2-4\left(x-2\right)^2=\left(9x^2+6x+1\right)-4\left(x^2-4x+4\right)\\ =9x^2-4x^2+6x+16x+1-16=5x^2+22x-15\\ =5x^2+25x-3x-15=5x\left(x+5\right)-3\left(x+5\right) =\left(x+5\right)\left(5x-3\right)\)
\(l,x^2-2xy+y^2-4m^2+4mn-n^2=\left(x-y\right)^2-\left[\left(2m\right)^2-2.2m.n+n^2\right]\\ =\left(x-y\right)^2-\left(2m-n\right)^2\\ =\left[\left(x-y\right)+\left(2m-n\right)\right].\left[\left(x-y\right)-\left(2m-n\right)\right]=\left(x+2m-y-n\right)\left(x+n-2m-y\right)\\ k,-4x^2+12xy-9y^2+25\\ =25-\left(4x^2-12xy+9y^2\right)\\ =5^2-\left[\left(2x\right)^2-2.2x.3y+\left(3y\right)^2\right]\\ =5^2-\left(2x-3y\right)^2\\ =\left(5-2x+3y\right)\left(5+2x-3y\right)\\ g,\left(ax+by\right)^2-\left(ay+bx\right)^2=\left[\left(ax+by\right)-\left(ay+bx\right)\right]\left[\left(ax+by\right)+\left(ay+bx\right)\right]\\ =\left(ax-ay+bx-by\right)\left(ax+ay+bx+by\right)\\ =\left[a\left(x-y\right)+b\left(x-y\right)\right].\left[a\left(x+y\right)+b\left(x+y\right)\right]\\ =\left(x-y\right)\left(a+b\right).\left(a+b\right)\left(x+y\right)\\ =\left(x^2-y^2\right)\left(a+b\right)^2\)
a) \(\left(3x-1\right)^2-16=\left(3x-1\right)^2-4^2=\left(3x-1-4\right)\left(3x-1+4\right)=\left(3x-5\right)\left(3x+3\right)\)
b) \(\left(5x-4\right)^2-49x^2=\left(5x-4\right)^2-\left(7x\right)^2=\left(5x-4-7x\right)\left(5x-4+7x\right)=\left(-2x-4\right)\left(12x-4\right)\)
c) \(\left(2x+5\right)^2-\left(x-9\right)^2=\left(2x+5-x+9\right)\left(2x+5+x-9\right)=\left(x+14\right)\left(3x-4\right)\)
d) \(\left(3x+1\right)^2-4\left(x-2\right)^2=\left[\left(3x+1\right)-2\left(x-2\right)\right]\left[\left(3x+1\right)+2\left(x-2\right)\right]\)
\(=\left(3x+1-2x+4\right)\left(3x+1+2x-4\right)\)
\(=\left(x+5\right)\left(5x-3\right)\)
e) \(9\left(2x+3\right)^2-4\left(x+1\right)^2\)
\(=\left[3\left(2x+3\right)-2\left(x+1\right)\right]\left[3\left(2x+3\right)+2\left(x+1\right)\right]\)
\(=\left(6x+9-2x-2\right)\left(6x+9+2x+2\right)\)
\(=\left(4x-7\right)\left(8x+11\right)\)
f) \(4b^2c^2-\left(b^2+c^2-a^2\right)^2\)
\(=\left(2bc\right)^2-\left(b^2+c^2-a^2\right)^2\)
\(=\left(2bc-b^2-c^2+a^2\right)\left(2bc+b^2+c^2-a^2\right)\)
g) \(\left(ax+by\right)^2-\left(ay+bx\right)^2\)
\(=\left(ax+by-ay-bx\right)\left(ax+by+ay+bx\right)\)
h) \(\left(a^2-b^2-5\right)^2-4\left(ab+2\right)^2\)
\(=\left[\left(a^2-b^2-5\right)-2\left(ab+2\right)\right]\left[\left(a^2-b^2-5\right)+2\left(ab+2\right)\right]\)
\(=\left(a^2-b^2-5-2ab-4\right)\left(a^2-b^2-5+2ab+4\right)\)
\(=\left(a^2-b^2-9-2ab\right)\left(a^2-b^2-1+2ab\right)\)