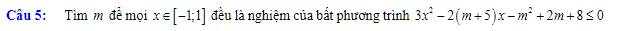Có:
\(3x^2-2\left(m+5\right)x-m^2+2m+8=0\Leftrightarrow x=m+2.hoặc.x=\dfrac{4-m}{3}\)
+) Với \(m+2>\dfrac{4-m}{3}\Leftrightarrow3m+6>4-m\Leftrightarrow m>-\dfrac{1}{2}\) ta có bất phương trình bất phương trình \(\Leftrightarrow\dfrac{4-m}{3}\le x\le m+2\)
Vậy tập nghiệm của bất phương trình là \(\left[\dfrac{4-m}{3};m+2\right]\)
=> mọi x \(\in\left[-1;1\right]\) đều là nghiệm của bất phương trình khi và chỉ khi
\(\left[-1;1\right]\subset\left[\dfrac{4-m}{3};m+2\right]\Leftrightarrow\left\{{}\begin{matrix}-1\ge\dfrac{4-m}{3}\\1\le m+2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}m\ge7\\m\ge-1\end{matrix}\right.\Rightarrow m\ge7\left(kết.hợp.đk:m>-\dfrac{1}{2}.thỏa.mãn\right)\)
+) Với \(m+2< \dfrac{4-m}{3}\Leftrightarrow m< -\dfrac{1}{2}\) ta có bất phương trình
\(\Leftrightarrow m+2\le x\le\dfrac{4-m}{3}\)
Vậy tập nghiệm của bất phương trình là \(\left[m+2;\dfrac{4-m}{3}\right]\)
=> mọi x \(\in\left[-1;1\right]\) đều là nghiệm của bất phương trình khi và chỉ khi
\(\left[-1;1\right]\subset\left[m+2;\dfrac{4-m}{3}\right]\\ \Leftrightarrow\left\{{}\begin{matrix}-1\ge m+2\\1\le\dfrac{4-m}{3}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}m\le-3\\m\le1\end{matrix}\right.\Rightarrow m\le-3\left(thỏa.mãn.đk:m< -\dfrac{1}{2}\right)\)
+) Với \(m=-\dfrac{1}{2}\) ta có bất phương trình \(\Leftrightarrow x=\dfrac{3}{2}\) nên \(m=-\dfrac{1}{2}\) không thỏa mãn yêu cầu bài toán.
Vậy \(m\in\) (\(-\infty\); -3] \(\cup\) [7; \(+\infty\)) là giá trị cần tìm
Có:
\(3x^2-2\left(m+5\right)x-m^2+2m+8=0\Leftrightarrow x=m+2.hoặc.x=\dfrac{4-m}{3}\)
+) Với \(m+2>\dfrac{4-m}{3}\Leftrightarrow3m+6>4-m\Leftrightarrow m>-\dfrac{1}{2}\) ta có bất phương trình bất phương trình \(\Leftrightarrow\dfrac{4-m}{3}\le x\le m+2\)
Vậy tập nghiệm của bất phương trình là \(\left[\dfrac{4-m}{3};m+2\right]\)
=> mọi x \(\in\left[-1;1\right]\) đều là nghiệm của bất phương trình khi và chỉ khi
\(\left[-1;1\right]\subset\left[\dfrac{4-m}{3};m+2\right]\Leftrightarrow\left\{{}\begin{matrix}-1\ge\dfrac{4-m}{3}\\1\le m+2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}m\ge7\\m\ge-1\end{matrix}\right.\Rightarrow m\ge7\left(kết.hợp.đk:m>-\dfrac{1}{2}.thỏa.mãn\right)\)