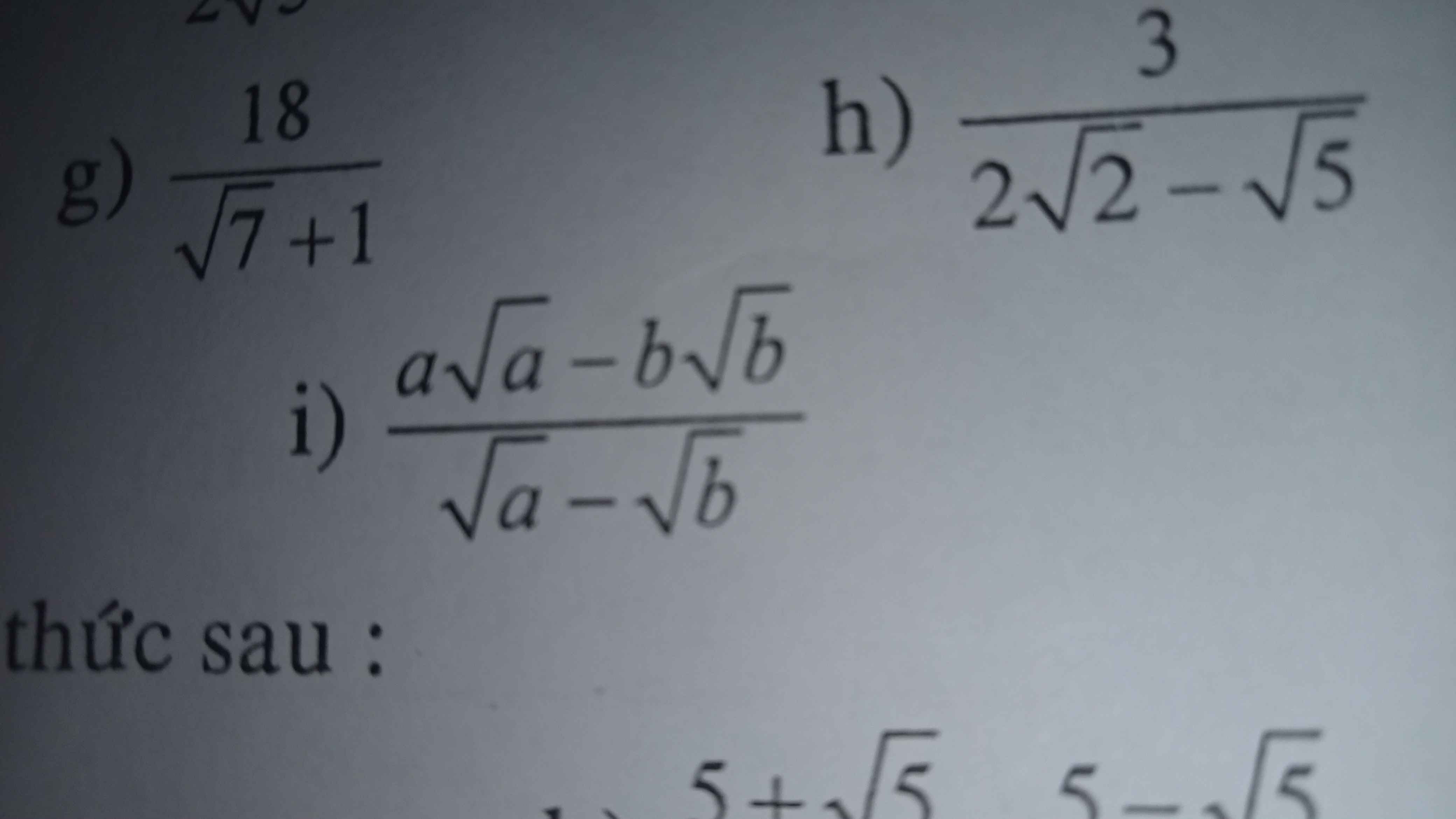Question

Answer 1

g: \(=3\left(\sqrt{7}-1\right)=3\sqrt{7}-3\)

b: \(=2\sqrt{2}+\sqrt{5}\)

i: \(=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(a+\sqrt{ab}+b\right)}{\sqrt{a}-\sqrt{b}}=a+\sqrt{ab}+b\)

Answer 2

g) \(\dfrac{18}{\sqrt{7}+1}=\dfrac{18\left(\sqrt{7}-1\right)}{7-1}=3\left(\sqrt{7}-1\right)=3\sqrt{7}-3\) 

h) \(\dfrac{3}{2\sqrt{2}-\sqrt{5}}=\dfrac{3\left(2\sqrt{2}+\sqrt{5}\right)}{8-5}=2\sqrt{2}+\sqrt{5}\)

i) a > 0 ; a \(\ne b\) . Ta có : \(\dfrac{a\sqrt{a}-b\sqrt{b}}{\sqrt{a}-\sqrt{b}}=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(a+b+\sqrt{ab}\right)}{\sqrt{a}-\sqrt{b}}=a+b+\sqrt{ab}\)