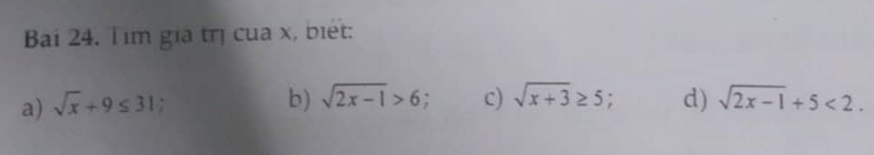\(\left(đk:x\ge0\right)\sqrt{x}+9\le31\Leftrightarrow\sqrt{x}\le22\Leftrightarrow x\le22\Rightarrow0\le x\le22\)
\(b;\left(đk:x\ge\dfrac{1}{2}\right)\sqrt{2x-1}>6\Leftrightarrow2x-1>36\Leftrightarrow x>\dfrac{37}{2}\)
\(c;đk:x\ge-3\Rightarrow\sqrt{x+3}\ge5\Leftrightarrow x+3\ge25\Leftrightarrow x\ge22\)
\(d;đk:x\ge\dfrac{1}{2};\sqrt{2x-1}< -3\left(vôli\right)\)
a: =>căn x<=22
=>0<=x<=484
b: =>2x-1>36
=>2x>37
hay x>37/2
c: =>x+3>=25
=>x>=22
d: =>căn (2x-1)<-3(vô lý)
\(\text{a},\sqrt{x}\) ≤ 22 đk x ≥ 0
x ≤ 484 KH vs đk
0 ≤ x ≤ 484
b, \(\left(\sqrt{2x-1}\right)^2>36\\ 2x-1>36\\ 2x>37\\ x>\dfrac{37}{2}\) đk x ≥ 1/2
KH đk => x > 37/2
\(c,\left(\sqrt{x+3}\right)^2\) ≥ 25 đk x ≥ -3
\(x+3\) ≥ 25
x ≥ 22 KH vs đk
=> x ≥ 22
d, x ≥ 1/2
\(\left(\sqrt{2x-1}\right)^2\) \(< -3\) ( vô lí )