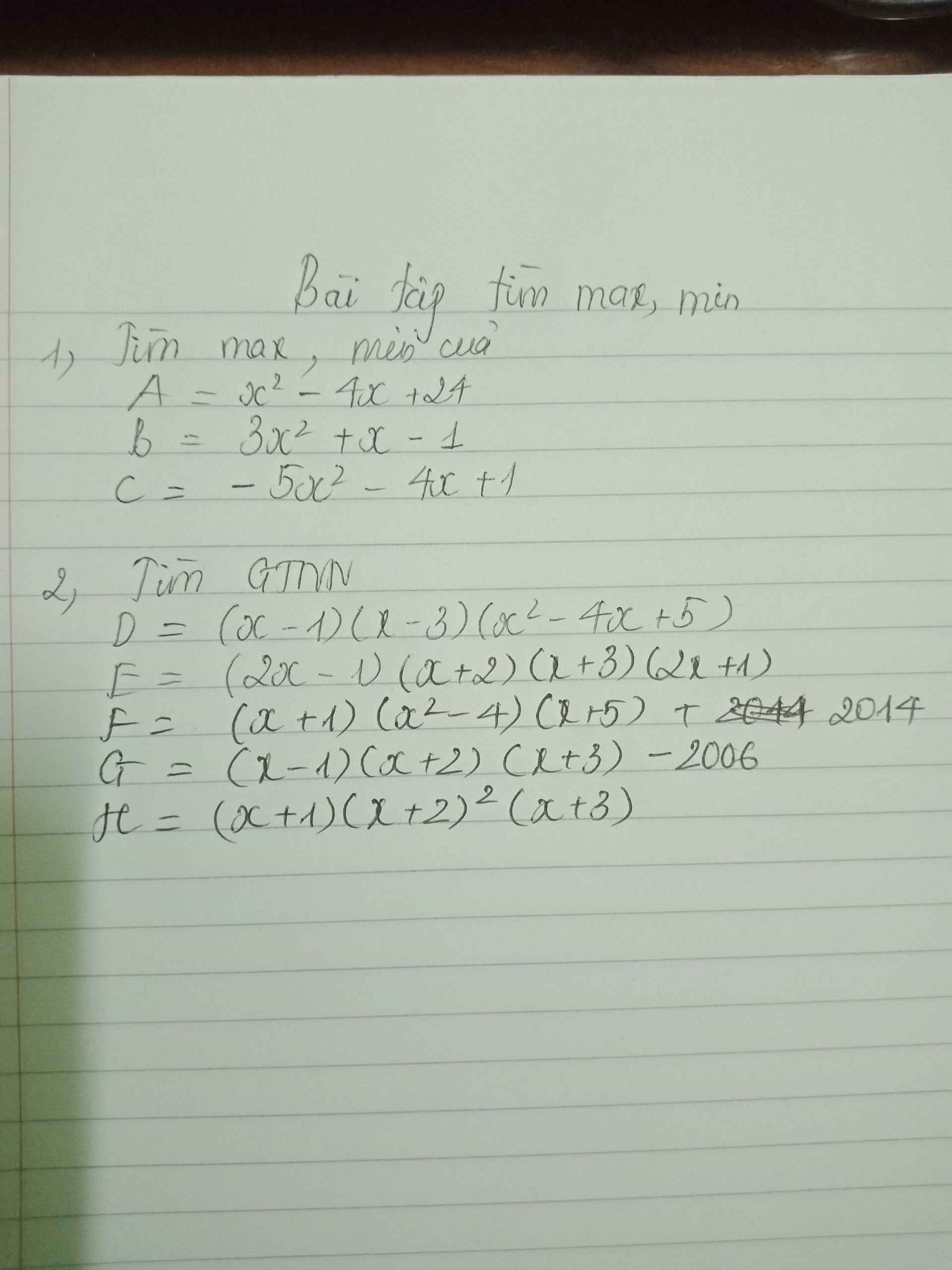1:
Ta có: \(A=x^2-4x+24\)
\(=x^2-4x+4+20\)
\(=\left(x-2\right)^2+20\ge20\forall x\)
Dấu '=' xảy ra khi x=2
1. Tìm max, min
\(A=x^2-4x+24=\left(x-2\right)^2+20\ge20\forall x\)
Dấu "=" xảy ra khi \(x-2=0\Leftrightarrow x=2\)
Vậy \(A_{min}=20\) khi \(x=2\)
\(B=3x^2+x-1=\left(x\sqrt{3}+\dfrac{1}{2\sqrt{3}}\right)^2-\dfrac{13}{12}\ge-\dfrac{13}{12}\forall x\)
Dấu "=" xảy ra khi \(x\sqrt{3}+\dfrac{1}{2\sqrt{3}}=0\Leftrightarrow x=-\dfrac{1}{6}\)
Vậy \(B_{min}=-\dfrac{13}{12}\) khi \(x=-\dfrac{1}{6}\)
\(C=-5x^2-4x+1=-\left(x\sqrt{5}+\dfrac{2}{\sqrt{5}}\right)^2+\dfrac{9}{5}\le\dfrac{9}{5}\forall x\)
Dấu "=" xảy ra khi \(x\sqrt{5}+\dfrac{2}{\sqrt{5}}=0\Leftrightarrow x=-\dfrac{2}{5}\)
Vậy \(C_{max}=\dfrac{9}{5}\) khi \(x=-\dfrac{2}{5}\)