Phân tích các đa thức sau thành nhân tử :
a) \(a^2-b^2-4a+4\)
b) \(x^2+2x-3\)
c) \(4x^2y^2-\left(x^2+y^2\right)^2\)
d) \(2a^3-54b^3\)
a) Thực hiện phép chia :
\(\left(2x^4-4x^3+5x^2+2x-3\right):\left(2x^2-1\right)\)
b) Chứng tỏ rằng thương tìm được trong phép chia trên luôn luôn dương với mọi giá trị của \(x\)
Chứng minh rằng hiệu các bình phương của hai số lẻ bất kì thì chia hết cho 8
Rút gọn rồi tính giá trị của biểu thức sau tại \(x=-\dfrac{1}{3}\)
\(\left[\dfrac{x+3}{\left(x-3\right)^2}+\dfrac{6}{x^2-9}-\dfrac{x-3}{\left(x+3\right)^2}\right]\left[1:\left(\dfrac{24x^2}{x^4-81}-\dfrac{12}{x^2+9}\right)\right]\)
Chứng minh rằng :
\(\dfrac{a^2}{a+b}+\dfrac{b^2}{b+c}+\dfrac{c^2}{c+a}=\dfrac{b^2}{a+b}+\dfrac{c^2}{b+c}+\dfrac{a^2}{c+a}\)
Tìm các giá trị nguyên của \(x\) để phân thức M có giá trị là một số nguyên :
\(M=\dfrac{10x^2-7x-5}{2x-3}\)
Giải các phương trình :
a) \(\dfrac{4x+3}{5}-\dfrac{6x-2}{7}=\dfrac{5x+4}{3}+3\)
b) \(\dfrac{3\left(2x-1\right)}{4}-\dfrac{3x+1}{10}+1=\dfrac{2\left(3x+2\right)}{5}\)
c) \(\dfrac{x+2}{3}+\dfrac{3\left(2x-1\right)}{4}-\dfrac{5x-3}{6}=x+\dfrac{5}{12}\)
Giải các phương trình :
a) \(\left|2x-3\right|=4\)
b) \(\left|3x-1\right|-x=2\)
a ) \(\left|2x-3\right|=4\left(1\right)\)
+ ) \(\left|2x-3\right|=2x-3.\)Khi \(2x-3\ge0\Leftrightarrow2x\ge3\Leftrightarrow x\ge\dfrac{3}{2}\)
\(\left(1\right)\Leftrightarrow2x-3=4\)
\(\Leftrightarrow2x=7\Leftrightarrow x=\dfrac{7}{2}\) ( thỏa )
+) \(\left|2x-3\right|=-2x+3.\) Khi \(2x-3< 0\Leftrightarrow2x< 3\Leftrightarrow x< \dfrac{3}{2}\)
\(\left(1\right)\Leftrightarrow-2x+3=4\)
\(\Leftrightarrow-2x=1\)
\(\Leftrightarrow x=-\dfrac{1}{2}\) ( thỏa )
b ) \(\left|3x-1\right|=3x-1.\)( 2 )
+ )Khi \(3x-1\ge0\Leftrightarrow3x\ge1\Leftrightarrow x\ge\dfrac{1}{3}.\)
\(\left(2\right)\Leftrightarrow3x-1-x=2\)
\(\Leftrightarrow2x=3\Leftrightarrow x=\dfrac{3}{2}\) ( thỏa )
+ ) \(\left|3x-1\right|=-3x+1.\)Khi \(3x-1< 0\Leftrightarrow3x< 1\Leftrightarrow x< \dfrac{1}{3}.\)
\(\left(2\right)\Leftrightarrow-3x+1-x=0\)
\(\Leftrightarrow-4x=-1\)
\(\Leftrightarrow x=\dfrac{1}{4}\) ( thỏa )
Vậy..........................
Trả lời bởi Võ Đông Anh Tuấn
Giải phương trình :
\(\dfrac{x+2}{98}+\dfrac{x+4}{96}=\dfrac{x+6}{94}+\dfrac{x+8}{92}\)
\(\dfrac{x+2}{98}+\dfrac{x+4}{96}=\dfrac{x+6}{94}+\dfrac{x+8}{92}\)
\(\Leftrightarrow\left(\dfrac{x+2}{98}+1\right)+\left(\dfrac{x+4}{96}+1\right)=\left(\dfrac{x+6}{94}+1\right)+\left(\dfrac{x+8}{92}+1\right)\)
\(\Leftrightarrow\dfrac{x+100}{98}+\dfrac{x+100}{96}-\dfrac{x+100}{94}+\dfrac{x+100}{92}=0\)
\(\Leftrightarrow\left(x+100\right)\left(\dfrac{1}{98}+\dfrac{1}{96}-\dfrac{1}{94}-\dfrac{1}{92}\right)=0\)
Vì : \(\dfrac{1}{98}+\dfrac{1}{96}-\dfrac{1}{94}-\dfrac{1}{92}\ne0\)
\(\Leftrightarrow x+100=0\Leftrightarrow x=-100\)
Vậy ...............
Trả lời bởi Võ Đông Anh TuấnGiải các phương trình :
a) \(\dfrac{1}{x+1}-\dfrac{5}{x-2}=\dfrac{15}{\left(x+1\right)\left(2-x\right)}\)
b) \(\dfrac{x-1}{x+2}-\dfrac{x}{x-2}=\dfrac{5x-2}{4-x^2}\)
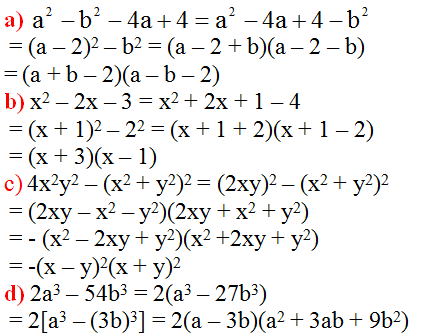
Trả lời bởi Phan Thùy Linh